[ad_1]
Dernière mise à jour le 6 août 2021
L’opérateur de Laplace a d’abord été appliqué à l’étude de la mécanique céleste, ou le mouvement des objets dans l’espace, par Pierre-Simon de Laplace, et en tant que tel a été nommé d’après lui.
L’opérateur de Laplace a depuis été utilisé pour décrire de nombreux phénomènes différents, des potentiels électriques à l’équation de diffusion pour l’écoulement de la chaleur et des fluides, en passant par la mécanique quantique. Il a également été refondu dans l’espace discret, où il a été utilisé dans des applications liées au traitement d’images et au clustering spectral.
Dans ce tutoriel, vous découvrirez une introduction douce au Laplacien.
Après avoir terminé ce tutoriel, vous saurez :
- La définition de l’opérateur de Laplace et son lien avec la divergence.
- Comment l’opérateur de Laplace se rapporte à la Hesse.
- Comment l’opérateur de Laplace continu a été refondu dans l’espace discret et appliqué au traitement d’images et au clustering spectral.
Commençons.

Une introduction douce au laplacien
Photo par Aziz Acharki, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; elles sont:
- Le Laplacien
- Le concept de divergence
- Le Laplacien Continu
- Le Laplacien discret
Conditions préalables
Pour ce tutoriel, nous supposons que vous savez déjà ce que sont :
Vous pouvez revoir ces concepts en cliquant sur les liens ci-dessus.
Le Laplacien
L’opérateur de Laplace (ou Laplacien, comme on l’appelle souvent) est la divergence du gradient d’une fonction.
Afin de mieux comprendre l’énoncé précédent, il est préférable de commencer par comprendre le concept de divergence.
Le concept de divergence
La divergence est un opérateur vectoriel qui opère sur un champ vectoriel. Ce dernier peut être considéré comme représentant un écoulement d’un liquide ou d’un gaz, où chaque vecteur dans le champ vectoriel représente un vecteur vitesse du fluide en mouvement.
En gros, la divergence mesure la tendance du fluide à s’accumuler ou à se disperser en un point…
– Page 432, Calcul simple et multivariable, 2020.
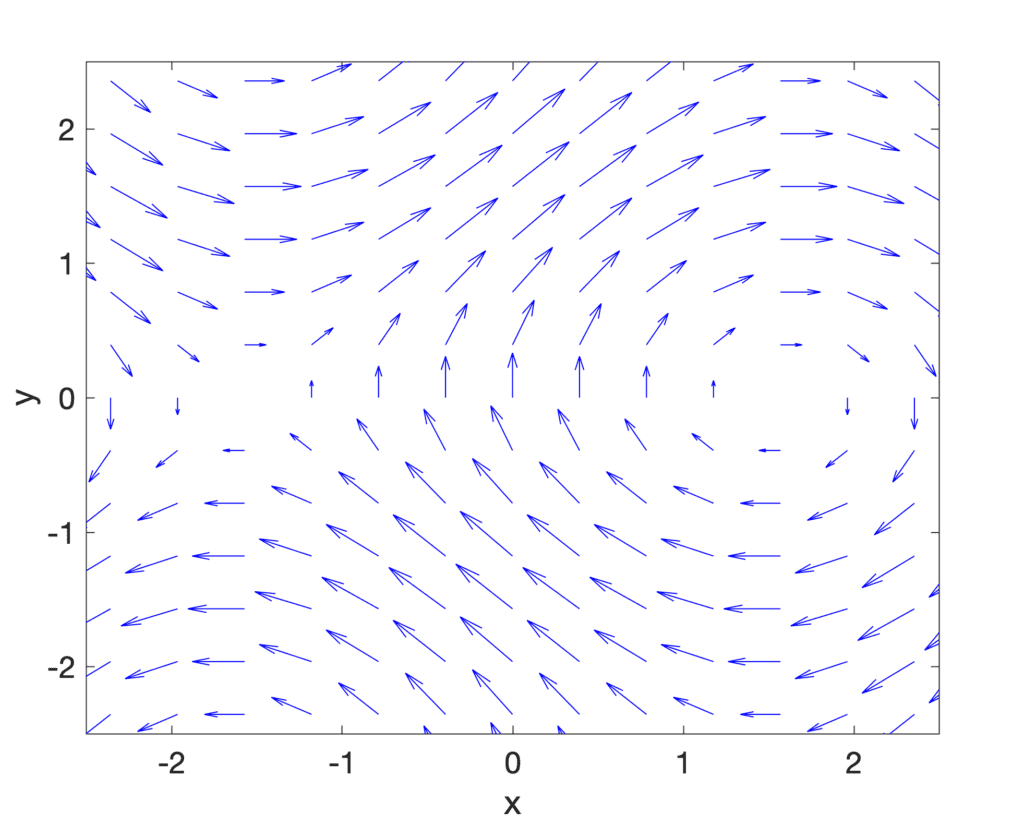
Une partie du champ vectoriel de (cos X, péché oui)
En utilisant l’opérateur nabla (ou del), , la divergence est notée ∇ . et produit une valeur scalaire lorsqu’elle est appliquée à un champ vectoriel, mesurant la quantité de fluide à chaque point. En coordonnées cartésiennes, la divergence d’un champ de vecteurs, F =F, g, h⟩, est donné par:
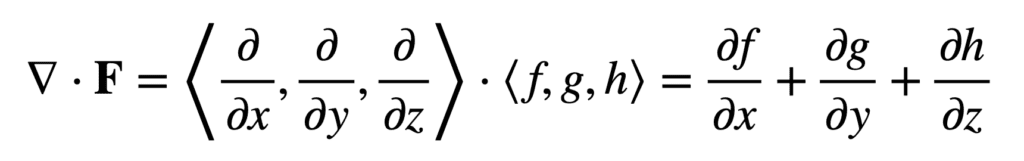
Bien que le calcul de divergence implique l’application de l’opérateur de divergence (plutôt qu’une opération de multiplication), le point dans sa notation rappelle le produit scalaire, qui implique la multiplication des composants de deux séquences de longueur égale (dans ce cas, ∇ et F) et la somme des termes résultants.
Le Laplacien Continu
Revenons à la définition du Laplacien.
Rappelons que le gradient d’une fonction à deux dimensions, F, est donné par:

Ensuite, le Laplacien (c’est-à-dire la divergence du gradient) de F peut être défini par la somme des dérivées partielles secondes non mélangées :
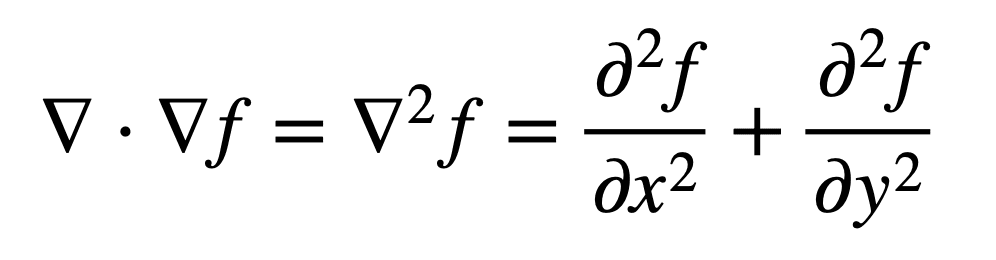
Elle peut, de manière équivalente, être considérée comme la trace (tr) du Hessien de la fonction, H(F). La trace définit la somme des éléments sur la diagonale principale d’un carré m×m matrice, qui dans ce cas est la Hessienne, et aussi la somme de ses valeurs propres. Rappelons que la matrice hessienne contient les dérivées partielles propres (ou non mélangées) sur la diagonale :
![]()
Une propriété importante de la trace d’une matrice est son invariance à une changement de base. Nous avons déjà défini le Laplacien en coordonnées cartésiennes. En coordonnées polaires, nous le définirions comme suit :
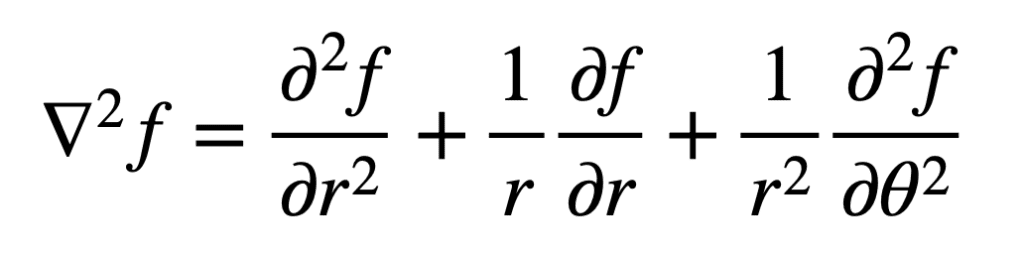
L’invariance de la trace à un changement de base signifie que le Laplacien peut être défini dans des espaces de coordonnées différents, mais il donnerait la même valeur à un moment donné (X, oui) dans l’espace de coordonnées cartésiennes, et au même point (r, ??) dans l’espace des coordonnées polaires.
Rappelons que nous avions également mentionné que la dérivée seconde peut nous fournir des informations concernant la courbure d’une fonction. Par conséquent, intuitivement, nous pouvons considérer que le Laplacien nous fournit également des informations sur la courbure locale d’une fonction, à travers cette sommation des dérivées secondes.
L’opérateur de Laplace continu a été utilisé pour décrire de nombreux phénomènes physiques, tels que les potentiels électriques et l’équation de diffusion pour le flux de chaleur.
Le Laplacien discret
Analogue à l’opérateur de Laplace continu, est l’opérateur discret, ainsi formulé afin d’être appliqué à une grille discrète de, disons, valeurs de pixels dans une image, ou à un graphique.
Voyons comment l’opérateur de Laplace peut être refondu pour les deux applications.
En traitement d’images, l’opérateur de Laplace est réalisé sous la forme d’un filtre numérique qui, appliqué à une image, peut être utilisé pour la détection des contours. En un sens, on peut considérer l’opérateur laplacien utilisé dans le traitement d’images pour, également, nous fournir des informations sur la manière dont la fonction courbe (ou virages) à un moment donné, (X, oui).
Dans ce cas, l’opérateur (ou filtre) laplacien discret est construit en combinant deux filtres de dérivée seconde à une dimension, en un seul à deux dimensions :
![]()
En apprentissage automatique, les informations fournies par l’opérateur de Laplace discret dérivées d’un graphique peuvent être utilisées à des fins de regroupement de données.
Considérons un graphique, g = (V, E), ayant un nombre fini de V sommets et E bords. Sa matrice laplacienne, L, peut être défini en termes de matrice de degrés, ré, contenant des informations sur la connectivité de chaque sommet, et la matrice d’adjacence, UNE, qui indique des paires de sommets adjacents dans le graphe :
L = ré – UNE
Le clustering spectral peut être effectué en appliquant une méthode de clustering standard (telle que k-means) sur les vecteurs propres de la matrice laplacienne, partitionnant ainsi les nœuds du graphe (ou les points de données) en sous-ensembles.
Un problème qui peut survenir en faisant cela concerne un problème d’évolutivité avec de grands ensembles de données, où la décomposition propre (ou l’extraction des vecteurs propres) de la matrice laplacienne peut être prohibitive. L’utilisation de l’apprentissage en profondeur a été proposée pour résoudre ce problème, où un réseau de neurones profonds est formé de telle sorte que ses sorties se rapprochent des vecteurs propres du graphe laplacien. Le réseau de neurones, dans ce cas, est entraîné à l’aide d’une approche d’optimisation contrainte, pour imposer l’orthogonalité des sorties du réseau.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Livres
Des articles
Papiers
Sommaire
Dans ce tutoriel, vous avez découvert une introduction douce au Laplacien.
Concrètement, vous avez appris :
- La définition de l’opérateur de Laplace et son lien avec la divergence.
- Comment l’opérateur de Laplace se rapporte à la Hesse.
- Comment l’opérateur de Laplace continu a été refondu dans l’espace discret et appliqué au traitement d’images et au clustering spectral.
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.