[ad_1]
Dernière mise à jour le 10 août 2021
Qu’il s’agisse d’un problème d’apprentissage supervisé ou d’un problème non supervisé, un algorithme d’optimisation fonctionnera en arrière-plan. Presque n’importe quel problème de classification, de régression ou de clustering peut être considéré comme un problème d’optimisation.
Dans ce tutoriel, vous découvrirez ce qu’est l’optimisation et les concepts qui s’y rapportent.
Après avoir terminé ce tutoriel, vous saurez :
- Qu’est-ce que la programmation mathématique ou l’optimisation
- Différence entre un problème de maximisation et de minimisation
- Différence entre les solutions optimales locales et globales
- Différence entre l’optimisation avec et sans contrainte
- Différence entre la programmation linéaire et non linéaire
- Exemples d’optimisation
Commençons.
Une introduction douce à l’optimisation. Photo de Mehtab Farooq, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; elles sont:
- Divers sujets d’introduction liés à l’optimisation
- Optimisation avec ou sans contrainte
- Contraintes d’égalité et d’inégalité
- Région possible
- Exemples d’optimisation en machine learning
Qu’est-ce que l’optimisation ou la programmation mathématique ?
En calcul et en mathématiques, le problème d’optimisation est également appelé programmation mathématique. Pour décrire ce problème en termes simples, c’est le mécanisme par lequel nous pouvons trouver un élément, une variable ou une quantité qui correspond le mieux à un ensemble de critères ou de contraintes donnés.
Maximisation vs. Problèmes de minimisation
Les cas les plus simples de problèmes d’optimisation sont la minimisation ou la maximisation des fonctions scalaires. Si nous avons une fonction scalaire d’une ou plusieurs variables, f(x_1, x_2, … x_n) alors ce qui suit est un problème d’optimisation :
Trouver x_1, x_2, …, x_n où f(x) est le minimum
Ou nous pouvons avoir un problème de maximisation équivalent.
Lorsque nous définissons des fonctions quantifiant les erreurs ou les pénalités, nous appliquons un problème de minimisation. En revanche, si un algorithme d’apprentissage construit une fonction modélisant la précision d’une méthode, nous maximiserions cette fonction.
De nombreux outils logiciels automatisés d’optimisation implémentent généralement soit un problème de maximisation, soit une tâche de minimisation, mais pas les deux. Par conséquent, nous pouvons convertir un problème de maximisation en un problème de minimisation (et vice versa) en ajoutant un signe négatif à f(x), c’est-à-dire,
Maximiser f(x) wrr x équivaut à Minimiser -f(x) wrt x
Les deux problèmes étant équivalents, nous ne parlerons que des problèmes de minimisation ou de maximisation dans la suite du didacticiel. Les mêmes règles et définitions s’appliquent à son équivalent.
Vs mondiaux. Points locaux optimaux
En apprentissage automatique, nous rencontrons souvent des fonctions hautement non linéaires avec un paysage complexe. Il est possible qu’il y ait un point où la fonction a la valeur la plus faible dans une petite région ou une région locale autour de ce point. Un tel point est appelé point minimum local.
Ceci est opposé au point minimum global, qui est un point où la fonction a le moins de valeur sur tout son domaine. La figure suivante montre les points maximaux locaux et globaux.

Points maximaux locaux et globaux
Non contraint Vs. Optimisation contrainte
Il existe de nombreux problèmes en apprentissage automatique, où nous nous intéressons à trouver le point optimal global sans aucune contrainte ni restriction sur la région dans l’espace. De tels problèmes sont appelés problèmes d’optimisation sans contraintes.
Parfois, nous devons résoudre un problème d’optimisation soumis à certaines contraintes. De tels problèmes d’optimisation sont appelés problèmes d’optimisation sous contraintes. Par exemple:
Minimiser x^2 + y^2 sous réserve. x + y <= 1
Voici des exemples d’optimisation contrainte :
- Trouver le minimum d’une fonction lorsque la somme des variables dans le domaine doit être égale à un
- Trouver le minimum d’une fonction telle que certains vecteurs soient normaux les uns aux autres
- Trouver le minimum d’une fonction telle que certaines variables de domaine se situent dans une certaine plage.
Région possible
Tous les points de l’espace où les contraintes sur le problème sont vraies constituent la région des possibles. Un algorithme d’optimisation recherche des points optimaux dans la région des possibles. La région réalisable pour les deux types de contraintes est illustrée dans la figure de la section suivante.
Pour un problème d’optimisation sans contrainte, le domaine entier de la fonction est une région réalisable.
Égalité contre. Contraintes d’inégalité
Les contraintes imposées dans un problème d’optimisation peuvent être des contraintes d’égalité ou des contraintes d’inégalité. La figure ci-dessous montre les deux types de contraintes.
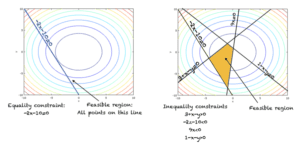
Contraintes d’égalité et d’inégalité
Vs linéaire. Programmation non linéaire
Un problème d’optimisation où la fonction est linéaire et toutes les contraintes d’égalité ou d’inégalité sont également des contraintes linéaires est appelé un problème de programmation linéaire.
Si la fonction objectif est non linéaire ou si une ou plusieurs contraintes sont non linéaires, alors nous avons un problème de programmation non linéaire.
Pour visualiser la différence entre les fonctions linéaires et non linéaires, vous pouvez consulter la figure ci-dessous.
Fonctions linéaires et non linéaires
Exemples d’optimisation dans l’apprentissage automatique
Vous trouverez ci-dessous quelques algorithmes d’apprentissage automatique bien connus qui utilisent l’optimisation. Vous devez garder à l’esprit que presque tous les algorithmes d’apprentissage automatique utilisent une sorte d’optimisation.
- Descente de gradient dans les réseaux de neurones (optimisation sans contrainte).
- Méthode des multiplicateurs de Lagrange dans les machines à vecteurs de support (optimisation contrainte).
- Analyse en composantes principales (optimisation contrainte)
- Clustering via l’algorithme de maximisation des attentes (optimisation contrainte)
- Régression logistique (optimisation sans contrainte)
- Algorithmes génétiques dans les algorithmes d’apprentissage évolutif (différentes variantes existent pour résoudre les problèmes d’optimisation à la fois contraints et non contraints).
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
- Méthode des multiplicateurs de Lagrange
- Techniques d’optimisation non linéaire
- La méthode du simplexe
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Thomas’ Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Sommaire
Dans ce tutoriel, vous avez découvert ce qu’est un problème de programmation mathématique ou d’optimisation. Concrètement, vous avez appris :
- Maximisation vs minimisation
- Optimisation avec ou sans contrainte
- Pourquoi l’optimisation est importante dans l’apprentissage automatique
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre