[ad_1]
Dernière mise à jour le 19 août 2021
Les matrices de Hesse appartiennent à une classe de structures mathématiques qui impliquent des dérivées du second ordre. Ils sont souvent utilisés dans les algorithmes d’apprentissage automatique et de science des données pour optimiser une fonction d’intérêt.
Dans ce tutoriel, vous découvrirez les matrices hessiennes, leurs discriminants correspondants, et leur signification. Tous les concepts sont illustrés par un exemple.
Après avoir terminé ce tutoriel, vous saurez :
- Matrices de jute
- Discriminants calculés via des matrices de Hesse
- Quelles informations sont contenues dans le discriminant
Commençons.

Une introduction douce aux matrices de Hesse. Photo de Beenish Fatima, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en trois parties ; elles sont:
- Définition de la matrice hessienne d’une fonction et du discriminant correspondant
- Exemple de calcul de la matrice de Hesse et du discriminant
- Ce que la Hesse et le discriminant nous disent de la fonction d’intérêt
Conditions préalables
Pour ce tutoriel, nous supposons que vous connaissez déjà :
Vous pouvez revoir ces concepts en cliquant sur les liens ci-dessus.
Qu’est-ce qu’une matrice de Hesse ?
La matrice hessienne est une matrice de dérivées partielles du second ordre. Supposons que nous ayons une fonction f de n variables, c’est-à-dire,
$$f : R^n rightarrow R$$
Le Hessien de f est donné par la matrice suivante à gauche. Le Hessien pour une fonction de deux variables est également montré ci-dessous à droite.
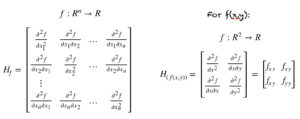
Hessian une fonction de n variables (gauche). Toile de jute de f(x,y) (à droite)
Nous savons déjà grâce à notre tutoriel sur les vecteurs de gradient que le gradient est un vecteur de dérivées partielles du premier ordre. Le Hessian est de même une matrice de dérivées partielles du second ordre formée de toutes les paires de variables dans le domaine de f.
Quel est le discriminant ?
Les déterminant de la Hesse est aussi appelé le discriminant de f. Pour une fonction à deux variables f(x, y), elle est donnée par :

Discriminant de f(x, y)
Exemples de matrices et de discriminants de Hesse
Supposons que nous ayons la fonction suivante :
g(x, y) = x^3 + 2y^2 + 3xy^2
Alors le Hessien H_g et le discriminant D_g sont donnés par :
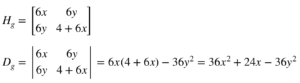
Hesse et discriminant de g(x, y) = x^3 + 2y^2 + 3xy^2
Évaluons le discriminant en différents points :
D_g(0, 0) = 0
D_g(1, 0) = 36 + 24 = 60
D_g(0, 1) = -36
D_g(-1, 0) = 12
Que signifient la toile de jute et le discriminant ?
Le Hessien et le discriminant correspondant sont utilisés pour déterminer les points extrêmes locaux d’une fonction. Leur évaluation aide à comprendre une fonction de plusieurs variables. Voici quelques règles importantes pour un point (a,b) où le discriminant est D(a,b) :
- La fonction f a un minimum local si f_xx(a, b) > 0 et le discriminant D(a,b) > 0
- La fonction f a un maximum local si f_xx(a, b) < 0 et le discriminant D(a,b) > 0
- La fonction f a un point selle si D(a, b) < 0
- Nous ne pouvons tirer aucune conclusion si D(a, b) = 0 et avons besoin de plus de tests
Exemple : g(x, y)
Pour la fonction g(x,y) :
- Nous ne pouvons tirer aucune conclusion pour le point (0, 0)
- f_xx(1, 0) = 6 > 0 et D_g(1, 0) = 60 > 0, donc (1, 0) est un minimum local
- Le point (0,1) est un point selle car D_g(0, 1) < 0
- f_xx(-1,0) = -6 < 0 et D_g(-1, 0) = 12 > 0, donc (-1, 0) est un maximum local
La figure ci-dessous montre un graphique de la fonction g(x, y) et ses contours correspondants.

Graphique de g(x,y) et contours de g(x,y)
Pourquoi la matrice de Hesse est-elle importante dans l’apprentissage automatique ?
La matrice de Hesse joue un rôle important dans de nombreux algorithmes d’apprentissage automatique, qui impliquent l’optimisation d’une fonction donnée. Bien qu’il puisse être coûteux à calculer, il contient des informations clés sur la fonction en cours d’optimisation. Il peut aider à déterminer les points de selle et l’extremum local d’une fonction. Il est largement utilisé dans la formation des réseaux de neurones et des architectures d’apprentissage en profondeur.
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
- Optimisation
- Valeurs propres de la matrice de Hesse
- Inverse de la matrice de Hesse et de l’entraînement des réseaux de neurones
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Thomas’ Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Sommaire
Dans ce tutoriel, vous avez découvert ce que sont les matrices de Hesse. Concrètement, vous avez appris :
- Matrice de Hesse
- Discriminant d’une fonction
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.