[ad_1]
Dernière mise à jour le 16 juillet 2021
La dérivée définit le taux auquel une variable change par rapport à une autre.
C’est un concept important qui se révèle extrêmement utile dans de nombreuses applications : dans la vie de tous les jours, le dérivé peut vous dire à quelle vitesse vous conduisez, ou vous aider à prévoir les fluctuations du marché boursier ; en apprentissage automatique, les dérivés sont importants pour l’optimisation des fonctions.
Ce tutoriel explorera différentes applications des dérivés, en commençant par les plus familières avant de passer à l’apprentissage automatique. Nous allons regarder de plus près ce que les dérivées nous disent sur les différentes fonctions que nous étudions.
Dans ce tutoriel, vous découvrirez différentes applications des dérivés.
Après avoir terminé ce tutoriel, vous saurez :
- L’utilisation de produits dérivés peut être appliquée à des problèmes de la vie réelle que nous trouvons autour de nous.
- L’utilisation de dérivées est essentielle en machine learning, pour l’optimisation des fonctions.
Commençons.

Applications des dérivés
Photo de Devon Janse van Rensburg, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; ils sont:
- Applications des dérivés dans la vie réelle
- Applications des dérivés dans les algorithmes d’optimisation
Applications des dérivés dans la vie réelle
Nous avons vu que les dérivés modélisent les taux de changement.
Les produits dérivés répondent à des questions telles que « À quelle vitesse ? » « Comment raide ? » et « Quelle sensibilité ? » Ce sont toutes des questions sur les taux de changement sous une forme ou une autre.
– Page 141, Pouvoirs infinis, 2019.
Ce taux de variation est noté,oui /X, définissant ainsi un changement dans la variable dépendante, 𝛿oui, par rapport à un changement de la variable indépendante, 𝛿X.
Commençons par l’une des applications les plus familières des dérivés que nous pouvons trouver autour de nous.
Chaque fois que vous montez dans votre voiture, vous assistez à une différenciation.
– Page 178, Calcul pour les nuls, 2016.
Quand nous disons qu’une voiture roule à 100 kilomètres à l’heure, nous aurions simplement indiqué son taux de variation. Le terme commun que nous utilisons souvent est la vitesse ou alors rapidité, bien qu’il soit préférable que nous distinguions d’abord les deux.
Dans la vie de tous les jours, nous utilisons souvent la vitesse et rapidité de manière interchangeable si nous décrivons le taux de changement d’un objet en mouvement. Cependant, cela n’est pas mathématiquement correct car la vitesse est toujours positive, alors que la vitesse introduit une notion de direction et, par conséquent, peut présenter à la fois des valeurs positives et négatives. Par conséquent, dans l’explication qui suit, nous considérerons la vitesse comme le concept le plus technique, défini comme :
vitesse =oui /t
Cela signifie que la vitesse donne le changement de position de la voiture,oui, dans un intervalle de temps, 𝛿t. En d’autres termes, la vitesse est la dérivée première de position par rapport au temps.
La vitesse de la voiture peut rester constante, par exemple si la voiture continue de rouler à 100 kilomètres à l’heure de manière constante, ou elle peut également changer en fonction du temps. Dans ce dernier cas, cela signifie que la fonction de vitesse elle-même change en fonction du temps, ou en termes plus simples, on peut dire que la voiture est accélérer. L’accélération est définie comme la dérivée première de la vitesse, v, et la dérivée seconde de la position, oui, par rapport au temps :
accélération =v /t = δ2oui /t2
Nous pouvons représenter graphiquement les courbes de position, de vitesse et d’accélération pour mieux les visualiser. Supposons que la position de la voiture, en fonction du temps, soit donnée par oui(t) = t3 – 8t2 + 40t:
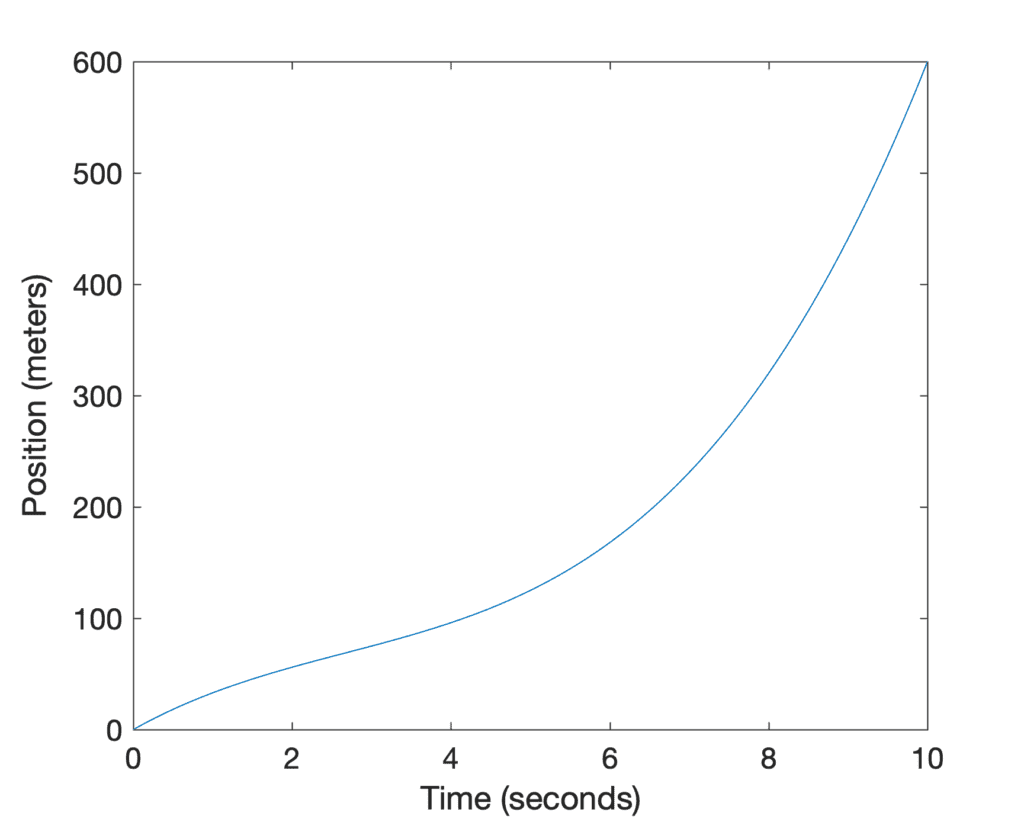
Tracé linéaire de la position de la voiture par rapport au temps
Le graphique indique que la position de la voiture change lentement au début du trajet, ralentissant légèrement jusqu’à environ t = 2,7 s, moment auquel son taux de changement s’accélère et continue d’augmenter jusqu’à la fin du trajet. Ceci est représenté par le graphique de la vitesse de la voiture :
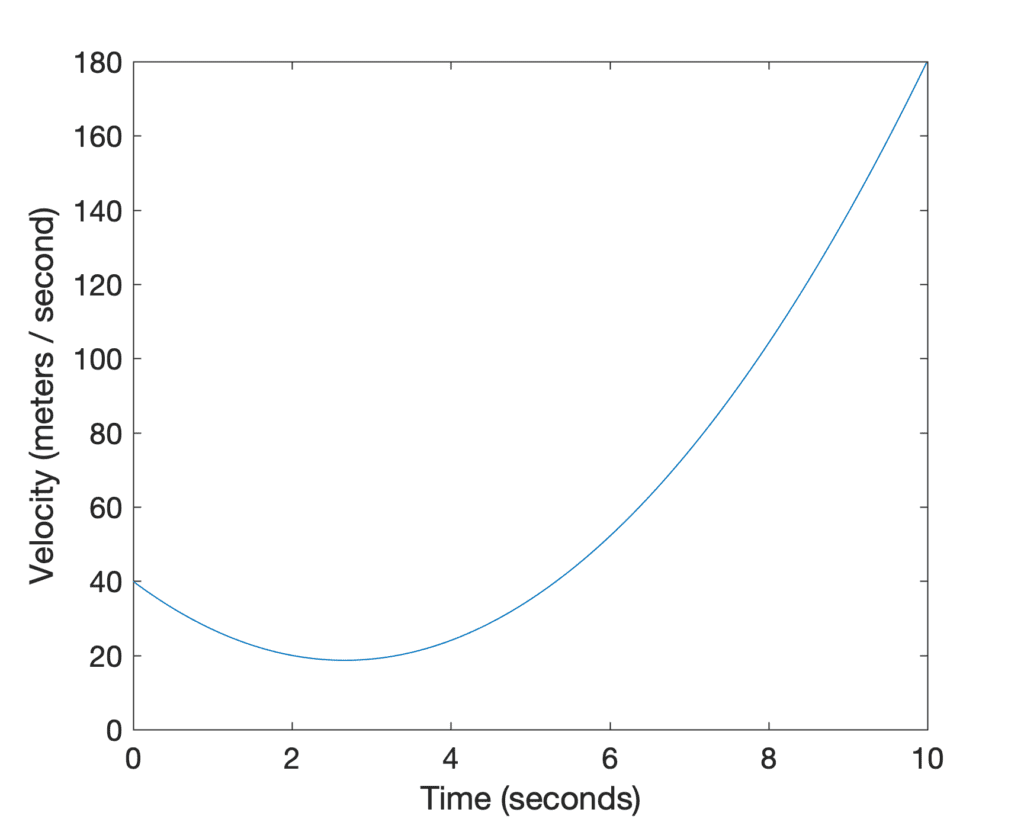
Tracé linéaire de la vitesse de la voiture en fonction du temps
Notez que la voiture conserve une vitesse positive tout au long du trajet, et c’est parce qu’elle ne change jamais de direction. Ainsi, si nous devions nous imaginer assis dans cette voiture en mouvement, le compteur de vitesse nous indiquerait les valeurs que nous venons de tracer sur le graphique de vitesse (puisque la vitesse reste positive tout au long, sinon il faudrait trouver la valeur absolue de la vitesse pour calculer la vitesse). Si nous devions appliquer la règle du pouvoir à oui(t) pour trouver sa dérivée, alors nous trouverions que la vitesse est définie par la fonction suivante :
v(t) = oui‘(t) = 3t2 – 16t + 40
On peut aussi tracer le graphique d’accélération :
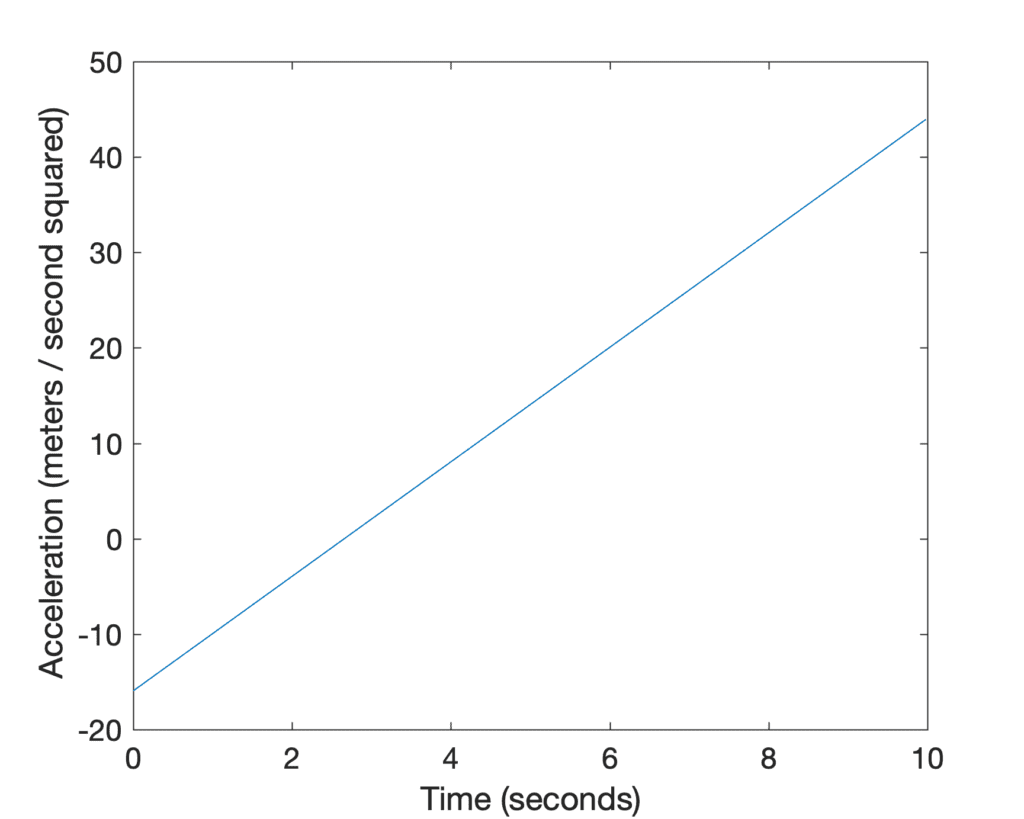
Tracé linéaire de l’accélération de la voiture contre le temps
Nous trouvons que le graphique est maintenant caractérisé par une accélération négative dans l’intervalle de temps, t =[027)secondesC’estparcequel’accélérationestladérivéedelavitesseetdanscetintervalledetempslavitessedelavoiturediminueSinousdevionsencoreunefoisappliquerlarègledupouvoirà[027)secondsThisisbecauseaccelerationisthederivativeofvelocityandwithinthistimeintervalthecar’svelocityisdecreasingIfwehadtoagainapplythepowerruletov(t) pour trouver sa dérivée, alors nous trouverions que l’accélération est définie par la fonction suivante :
une(t) = v‘(t) = 6t – 16
En regroupant toutes les fonctions, nous avons les éléments suivants :
oui(t) = t3 – 8t2 + 40t
v(t) = oui‘(t) = 3t2 – 16t + 40
une(t) = v‘(t) = 6t – 16
Si nous remplaçons t = 10s, on peut utiliser ces trois fonctions pour constater qu’à la fin du trajet, la voiture a parcouru 600m, sa vitesse est de 180 m/s, et elle accélère à 44 m/s2. Nous pouvons vérifier que toutes ces valeurs correspondent aux graphiques que nous venons de tracer.
Nous avons encadré cet exemple particulier dans le contexte de la recherche de la vitesse et de l’accélération d’une voiture. Mais il existe une pléthore de phénomènes de la vie réelle qui changent avec le temps (ou des variables autres que le temps), qui peuvent être étudiés en appliquant le concept de dérivées comme nous venons de le faire pour cet exemple particulier. Pour n’en citer que quelques-uns :
- Taux de croissance d’une population (qu’il s’agisse d’un ensemble d’humains ou d’une colonie de bactéries) au fil du temps, qui peut être utilisé pour prédire les changements dans la taille de la population dans un avenir proche.
- Changements de température en fonction de l’emplacement, qui peuvent être utilisés pour les prévisions météorologiques.
- Fluctuations du marché boursier dans le temps, qui peuvent être utilisées pour prédire le comportement futur du marché boursier.
Les dérivés fournissent également des informations importantes pour résoudre les problèmes d’optimisation, comme nous le verrons ensuite.
Applications des dérivés dans les algorithmes d’optimisation
Nous avions déjà vu qu’un algorithme d’optimisation, comme la descente de gradient, cherche à atteindre le minimum global d’une fonction d’erreur (ou de coût) en appliquant l’utilisation de dérivées.
Regardons de plus près ce que les dérivées nous disent sur la fonction d’erreur, en reprenant le même exercice que nous avons fait pour l’exemple de la voiture.
À cette fin, considérons la fonction de test unidimensionnelle suivante pour l’optimisation des fonctions :
F(X) = –X péché(X)
Nous pouvons appliquer la règle du produit à F(X) pour trouver sa dérivée première, notée F‘(X), puis appliquez à nouveau la règle de produit à F‘(X) pour trouver la dérivée seconde, notée F”(X):
F‘(X) = -péché(X) – X cos(X)
F”(X) = X péché(X) – 2 cos(X)
Nous pouvons tracer ces trois fonctions pour différentes valeurs de X pour les visualiser :

Ligne de tracé de fonction, F(X), sa dérivée première, F‘(X) et sa dérivée seconde, F“(X)
Semblable à ce que nous avons observé plus tôt pour l’exemple de la voiture, le graphique de la dérivée première indique comment F(X) change et de combien. Par exemple, une dérivée positive indique que F(X) est une fonction croissante, alors qu’une dérivée négative nous dit que F(X) est maintenant en baisse. Par conséquent, si dans sa recherche d’un minimum de fonction, l’algorithme d’optimisation effectue de petits changements à l’entrée en fonction de son taux d’apprentissage, :
x_nouveau = x – ε F‘(X)
L’algorithme peut alors réduire F(X) en se déplaçant dans le sens opposé (en inversant le signe) de la dérivée.
Nous pourrions également être intéressés par la recherche de la dérivée seconde d’une fonction.
Nous pouvons considérer la dérivée seconde comme la mesure de la courbure.
– Page 86, Apprentissage en profondeur, 2017.
Par exemple, si l’algorithme arrive à un point critique auquel la dérivée première est nulle, il ne peut pas distinguer entre ce point étant un maximum local, un minimum local, un point col ou une région plate basée sur F‘(X) seule. Cependant, lorsque la dérivée seconde intervient, l’algorithme peut dire que le point critique en question est un minimum local si la dérivée seconde est supérieure à zéro. Pour un maximum local, la dérivée seconde est inférieure à zéro. Par conséquent, la dérivée seconde peut informer l’algorithme d’optimisation dans quelle direction se déplacer. Malheureusement, ce test reste peu concluant pour les points-selles et les régions plates, pour lesquelles la dérivée seconde est nulle dans les deux cas.
Les algorithmes d’optimisation basés sur la descente de gradient n’utilisent pas de dérivées du second ordre et sont donc appelés algorithmes d’optimisation du premier ordre. Les algorithmes d’optimisation, tels que la méthode de Newton, qui exploitent l’utilisation de dérivées secondes, sont autrement appelés algorithmes d’optimisation du second ordre.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Livres
Résumé
Dans ce tutoriel, vous avez découvert différentes applications des dérivés.
Concrètement, vous avez appris :
- L’utilisation de produits dérivés peut être appliquée à des problèmes de la vie réelle que nous trouvons autour de nous.
- L’utilisation de dérivées est essentielle en machine learning, pour l’optimisation des fonctions.
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.