[ad_1]
Les dérivées partielles et les vecteurs de gradient sont très souvent utilisés dans les algorithmes d’apprentissage automatique pour trouver le minimum ou le maximum d’une fonction. Les vecteurs de gradient sont utilisés dans l’apprentissage des réseaux de neurones, la régression logistique et de nombreux autres problèmes de classification et de régression.
Dans ce tutoriel, vous découvrirez les dérivées partielles et le vecteur gradient.
Après avoir terminé ce tutoriel, vous saurez :
- Fonction de plusieurs variables
- Ensembles de niveaux, contours et graphiques d’une fonction de deux variables
- Dérivées partielles d’une fonction de plusieurs variables
- Vecteur de dégradé et sa signification
Commençons.

Une introduction douce aux dérivés partiels et aux vecteurs de gradient. Une photo d’Atif Gulzar, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en trois parties ; ils sont:
- Fonction de plusieurs variables
- Ensembles de niveaux
- Contours
- Graphiques
- Définition des dérivées partielles
- Vecteur de dégradé
- Que représente le vecteur de gradient
Une fonction de plusieurs variables
Vous pouvez revoir le concept d’une fonction et une fonction de plusieurs variables dans ce tutoriel. Nous fournirons plus de détails sur les fonctions de plusieurs variables ici.
Une fonction de plusieurs variables a les propriétés suivantes :
- Son domaine est un ensemble de n-uplets donné par (x_1, x_2, x_3, …, x_n)
- Sa plage est un ensemble de nombres réels
Par exemple, ce qui suit est une fonction de deux variables (n=2) :
f_1(x,y) = x + y
Dans la fonction ci-dessus, x et y sont les variables indépendantes. Leur somme détermine la valeur de la fonction. Le domaine de cette fonction est l’ensemble de tous les points sur le plan cartésien XY. Le tracé de cette fonction nécessiterait un tracé dans l’espace 3D, avec deux axes pour les points d’entrée (x,y) et le troisième représentant les valeurs de f.
Voici un autre exemple de fonction à deux variables. f_2(x,y) = x*x + y*oui
Pour garder les choses simples, nous allons faire des exemples de fonctions de deux variables. Bien sûr, dans l’apprentissage automatique, vous rencontrerez des fonctions de centaines de variables. Les concepts liés aux fonctions de deux variables peuvent être étendus à ces cas.
Ensembles de niveaux et graphique d’une fonction de deux variables
L’ensemble des points dans un plan, où une fonction f(x,y) a une valeur constante, c’est-à-dire que f(x,y)=c est l’ensemble de niveaux ou la courbe de niveau de f.
Par exemple, pour la fonction f_1, tous les points (x,y) qui satisfont à l’équation ci-dessous définissent un niveau défini pour f_1 :
x + y = 1
Nous pouvons voir que cet ensemble de niveaux a un ensemble infini de points, par exemple (0,2), (1,1), (2, 0), etc. Cet ensemble de niveaux définit une ligne droite dans le plan XY.
En général, tous les ensembles de niveaux de f_1 définissent des lignes droites de la forme (c est une constante réelle) :
x + y = c
De même, pour la fonction f_2, un exemple de level set est :
X*x + y*y = 1
Nous pouvons voir que tout point situé sur un cercle de rayon 1 de centre (0,0) satisfait l’expression ci-dessus. Par conséquent, cet ensemble de niveaux se compose de tous les points qui se trouvent sur ce cercle. De même, tout level set de f_2 satisfait l’expression suivante (c est une constante réelle >= 0) :
X*x + y*y = c
Par conséquent, tous les ensembles de niveaux de f_2 sont des cercles dont le centre est à (0,0), chaque ensemble de niveaux ayant son propre rayon.
Le graphe de la fonction f(x,y) est l’ensemble de tous les points (x,y,f(x,y)). On l’appelle aussi surface z=f(x,y). Les graphiques de f_1 et f_2 sont présentés ci-dessous (côté gauche).
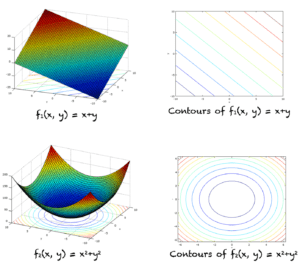
Les fonctions f_1 et f_2 et leurs contours correspondants
Contours d’une fonction de deux variables
Supposons que nous ayons une fonction f(x,y) de deux variables. Si nous coupons la surface z=f(x,y) en utilisant un plan z=c, alors nous obtenons l’ensemble de tous les points qui satisfont f(x,y) = c. La courbe de contour est l’ensemble des points qui satisfont f(x,y)=c, dans le plan z=c. Ceci est légèrement différent du level set, où la courbe de niveau est directement définie dans le plan XY. Cependant, de nombreux livres traitent les contours et les courbes de niveau de la même manière.
Les contours de f_1 et f_2 sont montrés dans la figure ci-dessus (côté droit).
Dérivées partielles et gradients
La dérivée partielle d’une fonction f par rapport à la variable x est notée ∂f/∂x. Son expression peut être déterminée en différenciant f wrtx Par exemple pour les fonctions f_1 et f_2, on a :
f_1/∂x = 1
f_2/∂x = 2x
∂f_1/∂x représente le taux de variation de f_1 par rapport à x. Pour toute fonction f(x,y), ∂f/∂x représente le taux de variation de f par rapport à la variable x.
Il en est de même pour ∂f/∂y. Il représente le taux de variation de f par rapport à y. Vous pouvez consulter la définition formelle des dérivées partielles dans ce tutoriel.
Lorsque nous trouvons les dérivées partielles par rapport à toutes les variables indépendantes, nous nous retrouvons avec un vecteur. Ce vecteur est appelé vecteur gradient de f noté ∇f(x,y). Une expression générale pour les gradients de f_1 et f_2 est donnée par (ici i,j sont des vecteurs unitaires parallèles à l’axe des coordonnées) :
∇f_1(x,y) = ∂f_1/∂xi + ∂f_1/∂yj = i+j
∇f_2(x,y) = ∂f_2/∂xi + ∂f_2/∂yj = 2xi + 2yj
A partir de l’expression générale du gradient, on peut évaluer le gradient en différents points de l’espace. Dans le cas de f_1, le vecteur gradient est une constante, c’est-à-dire
i+j
Peu importe où nous nous trouvons dans l’espace tridimensionnel, la direction et l’amplitude du vecteur gradient restent inchangées.
Pour la fonction f_2, ∇f_2(x,y) change avec les valeurs de (x,y). Par exemple, en (1,1) et (2,1) la pente de f_2 est donnée par les vecteurs suivants :
f_2(1,1) = 2i + 2j
f_2(2,1) = 4i + 2j
Qu’indique le vecteur de gradient en un point ?
Le vecteur gradient d’une fonction de plusieurs variables en tout point indique la direction du taux de changement maximum.
Nous pouvons relier le vecteur gradient à la ligne tangente. Si nous nous tenons à un point dans l’espace et que nous élaborons une règle qui nous dit de marcher le long de la tangente au contour en ce point. Cela signifie que, où que nous soyons, nous trouvons la ligne tangente au contour en ce point et nous marchons le long de celle-ci. Si nous marchons en suivant cette règle, nous finirons par marcher le long du contour de f. La valeur de la fonction ne changera jamais car la valeur de la fonction est constante sur le contour de f.
Le vecteur gradient, d’autre part, est normal à la ligne tangente et pointe vers la direction du taux d’augmentation maximum. Si nous marchons dans la direction du gradient, nous commencerons à rencontrer le prochain point où la valeur de la fonction serait supérieure à la précédente.
Le sens positif du gradient indique le sens du taux d’augmentation maximum, tandis que le sens négatif indique le sens du taux de diminution maximum. La figure suivante montre la direction positive du vecteur gradient en différents points des contours de la fonction f_2. La direction du gradient positif est indiquée par la flèche rouge. La ligne tangente à un contour est représentée en vert.
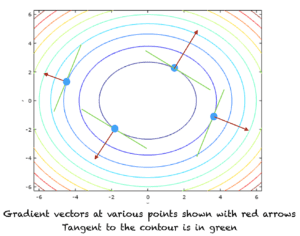
Les contours et la direction des vecteurs de gradient
Pourquoi le vecteur de gradient est-il important dans l’apprentissage automatique ?
Le vecteur de gradient est très important et fréquemment utilisé dans les algorithmes d’apprentissage automatique. Dans les problèmes de classification et de régression, nous définissons normalement la fonction d’erreur quadratique moyenne. Suivre le sens négatif du gradient de cette fonction nous amènera à trouver le point où cette fonction a une valeur minimale.
Il en va de même pour les fonctions, où leur maximisation permet d’obtenir une précision maximale. Dans ce cas, nous suivrons la direction du taux d’augmentation maximum de cette fonction ou la direction positive du vecteur gradient.
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
- Descente en pente / montée en pente
- Matrice de Hesse
- Jacobien
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Thomas’ Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Résumé
Dans ce tutoriel, vous avez découvert quelles sont les fonctions de plusieurs variables, les dérivées partielles et le vecteur gradient. Concrètement, vous avez appris :
- Fonction de plusieurs variables
- Contours d’une fonction de plusieurs variables
- Ensembles de niveaux d’une fonction de plusieurs variables
- Dérivées partielles d’une fonction de plusieurs variables
- Vecteur de dégradé et sa signification
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.