[ad_1]
De nombreux domaines du calcul nécessitent une compréhension des fonctions continues. Le les caractéristiques des fonctions continues et l’étude des points de discontinuité sont d’un grand intérêt pour la communauté mathématique. En raison de leurs propriétés importantes, les fonctions continues ont des applications pratiques dans les algorithmes d’apprentissage automatique et les méthodes d’optimisation.
Dans ce tutoriel, vous découvrirez quelles sont les fonctions continues, leurs propriétés et deux théorèmes importants dans l’étude des algorithmes d’optimisation, à savoir le théorème des valeurs intermédiaires et le théorème des valeurs extrêmes.
Après avoir terminé ce tutoriel, vous saurez :
- Définition des fonctions continues
- Théorème des valeurs intermédiaires
- Théorème des valeurs extrêmes
Commençons.
Une introduction en douceur aux fonctions continues Photo de Jeeni Khala, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en 2 parties ; ils sont:
- Définition des fonctions continues
- Définition informelle
- Définition formelle
- Théorèmes
- Théorème des valeurs intermédiaires
- Théorème des valeurs extrêmes
Conditions préalables
Ce tutoriel nécessite une compréhension du concept de limites. Pour vous rafraîchir la mémoire, vous pouvez jeter un œil aux limites et à la continuité, où les fonctions continues sont également brièvement définies. Dans ce tutoriel, nous allons entrer dans plus de détails.
Nous utiliserons également des intervalles. Ainsi, les crochets signifient des intervalles fermés (inclure les points limites) et les parenthèses signifient des intervalles ouverts (ne pas inclure les points limites), par exemple,
- [a,b] signifie a<=x<=b
- (a,b) signifie a
- [a,b) means a<=x<b
From the above, you can note that an interval can be open on one side and closed on the other.
As a last point, we’ll only be discussing real functions defined over real numbers. We won’t be discussing complex numbers or functions defined on the complex plane.
An Informal Definition of Continuous Functions
Suppose we have a function f(x). We can easily check if it is continuous between two points a and b, if we can plot the graph of f(x) without lifting our hand. As an example, consider a straight line defined as:
f(x)=2x+1
We can draw the straight line between [0,1] sans lever la main. En fait, nous pouvons tracer cette ligne entre deux valeurs de x et nous n’aurons pas à lever la main (voir figure ci-dessous). Par conséquent, cette fonction est continue sur tout le domaine des nombres réels. Voyons maintenant ce qui se passe lorsque nous traçons la fonction ceil :
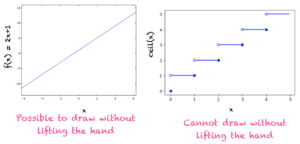
Fonction continue (à gauche) et non une fonction continue (à droite)
La fonction ceil a une valeur de 1 sur l’intervalle (0,1], par exemple, ceil(0.5)= 1, ceil(0.7) = 1, et ainsi de suite. En conséquence, la fonction est continue sur le domaine ( 0,1]. Si l’on ajuste l’intervalle à (0,2], ceil(x) passe à 2 dès que x>1. Pour tracer ceil(x) pour le domaine (0,2], il faut maintenant lever notre main et recommencer à tracer à x = 2. Par conséquent, la fonction ceil n’est pas une fonction continue.
Si la fonction est continue sur tout le domaine des nombres réels, alors c’est un continu fonctionner dans son ensemble, sinon, il n’est pas continu dans son ensemble. Pour le dernier type de fonctions, nous pouvons vérifier sur quel intervalle elles sont continues.
Une définition formelle
Une fonction f(x) est continue en un point a, si la valeur de la fonction tend vers f(a) lorsque x tend vers a. Par conséquent, pour tester la continuité d’une fonction en un point x=a, vérifiez les éléments suivants :
- f(a) devrait exister
- f(x) a une limite lorsque x s’approche de a
- La limite de f(x) comme x->a est égale à f(a)
Si tout ce qui précède est vrai, alors la fonction est continue au point a.
Exemples
Certains exemples sont répertoriés ci-dessous et également illustrés dans la figure :
- f(x) = 1/x n’est pas continu car il n’est pas défini à x=0. Cependant, la fonction est continue pour le domaine x>0.
- Toutes les fonctions polynomiales sont des fonctions continues.
- Les fonctions trigonométriques sin(x) et cos(x) sont continu et osciller entre les valeurs -1 et 1.
- La fonction trigonométrique tan(x) n’est pas continue car indéfinie en x=𝜋/2, x=-𝜋/2, etc.
- sqrt(x) n’est pas continu car il n’est pas défini pour x<0.
- |x| est continue partout.

Exemples de fonctions continues et de fonctions discontinues
Connexion de la continuité avec les dérivés de fonction
De la définition de la continuité en termes de limites, nous avons une définition alternative. f(x) est continue en x, si :
f(x+h)-f(x)→ 0 quand (h→0)
Regardons la définition d’une dérivée :
f'(x) = lim(h→0) (f(x+h)-f(x))/h
Donc, si f'(x) existe en un point a, alors la fonction est continue en a. L’inverse n’est pas toujours vrai. Une fonction peut être continue en un point a, mais f'(a) peut ne pas exister. Par exemple, dans le graphique ci-dessus |x| est continue partout. On peut le dessiner sans lever la main, cependant à x=0 sa dérivée n’existe pas à cause du virage brusque de la courbe.
Le théorème des valeurs intermédiaires énonce que :
Si:
- la fonction f(x) est continue sur [a,b]
- et f(a) <= K <= f(b)
ensuite:
- Il existe un point c entre a et b, c’est-à-dire a<=c<=b tel que f(c) = K
En termes très simples, ce théorème dit que si une fonction est continue sur [a,b], alors toutes les valeurs de la fonction entre f(a) et f(b) existeront dans cet intervalle, comme le montre la figure ci-dessous.
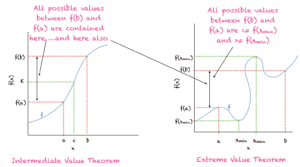
Illustration du théorème des valeurs intermédiaires (à gauche) et du théorème des valeurs extrêmes (à droite)
Théorème des valeurs extrêmes
Ce théorème dit que :
Si:
- la fonction f(x) est continue sur [a,b]
ensuite:
- Il y a des points x_min et x_max à l’intérieur de l’intervalle [a,b], c’est à dire,
- et la fonction f(x) a une valeur minimale f(x_min), et une valeur maximale f(x_max), c’est-à-dire,
- f(x_min)<=f(x)<=f(x_max) quand a<=x<=b
En termes simples, une fonction continue a toujours une valeur minimale et maximale dans un intervalle, comme le montre la figure ci-dessus.
Fonctions continues et optimisation
Les fonctions continues sont très importantes dans l’étude des problèmes d’optimisation. Nous pouvons voir que le théorème des valeurs extrêmes garantit que dans un intervalle, il y aura toujours un point où la fonction a une valeur maximale. La même chose peut être dite pour une valeur minimale. De nombreux algorithmes d’optimisation sont dérivés de cette propriété fondamentale et peuvent effectuer des tâches étonnantes.
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
- Séquences convergentes et divergentes
- Définitions de Weierstrass et Jordan des fonctions continues basées sur des constantes infiniment petites
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Thomas’ Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Résumé
Dans ce tutoriel, vous avez découvert le concept de fonctions continues.
Concrètement, vous avez appris :
- Quelles sont les fonctions continues
- Les définitions formelles et informelles des fonctions continues
- Points de discontinuité
- Théorème des valeurs intermédiaires
- Théorème des valeurs extrêmes
- Pourquoi les fonctions continues sont importantes
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.