[ad_1]
Dernière mise à jour le 19 juin 2021
Calcul est l’étude mathématique du changement.
L’efficacité du calcul pour résoudre un problème compliqué mais continu réside dans sa capacité à découper le problème en parties infiniment plus simples, à les résoudre séparément, puis à les reconstruire dans l’ensemble d’origine. Cette stratégie peut être appliquée pour étudier tous les éléments continus qui peuvent être tranchés de cette manière, que ce soit les courbures de formes géométriques, ainsi que la trajectoire d’un objet en vol, ou un intervalle de temps.
Dans ce tutoriel, vous découvrirez les origines du calcul et ses applications.
Après avoir terminé ce tutoriel, vous saurez :
- Qu’est-ce que le calcul ?
- Comment le calcul peut-il être appliqué au monde réel ?
Commençons.

Qu’est-ce que le calcul ?
Photo de Stephen Lammens, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; elles sont:
- Calcul
- Applications du calcul
Calcul
Calcul est un mot latin pour pierre ou caillou.
L’utilisation de ce mot s’est infiltrée dans les mathématiques à partir de l’ancienne pratique consistant à utiliser de petites pierres pour effectuer des calculs, tels que l’addition et la multiplication. Alors que l’utilisation de ce mot a, avec le temps, disparu du titre de nombreuses méthodes de calcul, une branche importante des mathématiques l’a tellement conservé que nous l’appelons maintenant le Calcul.
Le calcul, comme d’autres formes de mathématiques, est bien plus qu’un langage ; c’est aussi un système de raisonnement incroyablement puissant.
– Page xii, Pouvoirs infinis, 2019.
Le calcul a mûri à partir de la géométrie.
Au début, la géométrie était concernée par les lignes droites, les plans et les angles, reflétant ses origines utilitaires dans la construction de rampes et de pyramides, entre autres utilisations. Néanmoins, les géomètres se sont retrouvés sans outils pour l’étude des cercles, des sphères, des cylindres et des cônes. Les surfaces et les volumes de ces formes courbes se sont avérés beaucoup plus difficiles à analyser que les formes rectilignes faites de lignes droites et de plans plats. Malgré sa réputation de complexité, la méthode de calcul est née d’une quête de simplicité, en décomposant des problèmes compliqués en parties plus simples.
De retour vers 250 avant notre ère dans la Grèce antique, c’était une petite startup mathématique à chaud consacrée au mystère des courbes.
– Page 3, Pouvoirs infinis, 2019.
Pour ce faire, le calcul tournait autour de l’utilisation contrôlée de l’infini comme pont entre la courbe et la droite.
Le principe de l’infini
Pour faire la lumière sur une forme, un objet, un mouvement, un processus ou un phénomène continus, peu importe à quel point cela peut paraître sauvage et compliqué, réimaginez-le comme une série infinie de pièces plus simples, analysez-les, puis ajoutez les résultats pour donner un sens de l’ensemble originel.
– Page xvi, Pouvoirs infinis, 2019.
Pour saisir un peu mieux ce concept, imaginez-vous voyager sur un vaisseau spatial vers la lune. Lorsque vous regardez la lune vers l’extérieur depuis la terre, son contour semble sans aucun doute incurvé. Mais à mesure que vous vous rapprochez et que des parties plus petites du contour commencent à remplir le port de visualisation, la courbure s’atténue et devient moins définie. Finalement, la quantité de courbure devient si petite que les parties infiniment petites du contour apparaissent comme une ligne droite. Si nous devions découper la forme circulaire de la lune le long de ces parties infiniment petites de son contour, puis disposer les tranches infiniment petites dans un rectangle, alors nous serions capables de calculer son aire : en multipliant sa largeur par sa hauteur.
C’est l’essence du calcul : la percée selon laquelle si l’on regarde une forme incurvée au microscope, la partie de sa courbure sur laquelle on zoome apparaîtra droite et plate. Ainsi, l’analyse d’une forme courbe est, en principe, rendue possible par l’assemblage de ses nombreuses pièces droites.
Le calcul peut donc être considéré comme comprenant deux phases : la coupe et la reconstruction.
En termes mathématiques, le processus de coupe implique toujours une soustraction infiniment fine, qui est utilisée pour quantifier les différences entre les pièces. En conséquence, cette moitié du sujet est appelée calcul différentiel. Le processus de remontage implique toujours un ajout infini, qui réintègre les pièces dans l’ensemble d’origine. Cette moitié du sujet est appelée calcul intégral.
– Page xv, Pouvoirs infinis, 2019.
Dans cet esprit, reprenons notre exemple simple.
Supposons que nous ayons découpé la forme circulaire de la lune en morceaux plus petits et que nous ayons réarrangé les morceaux les uns à côté des autres.
La forme que nous avons formée est semblable à un rectangle ayant une largeur égale à la moitié de la circonférence du cercle, C/2, et une hauteur égale au rayon du cercle, r.
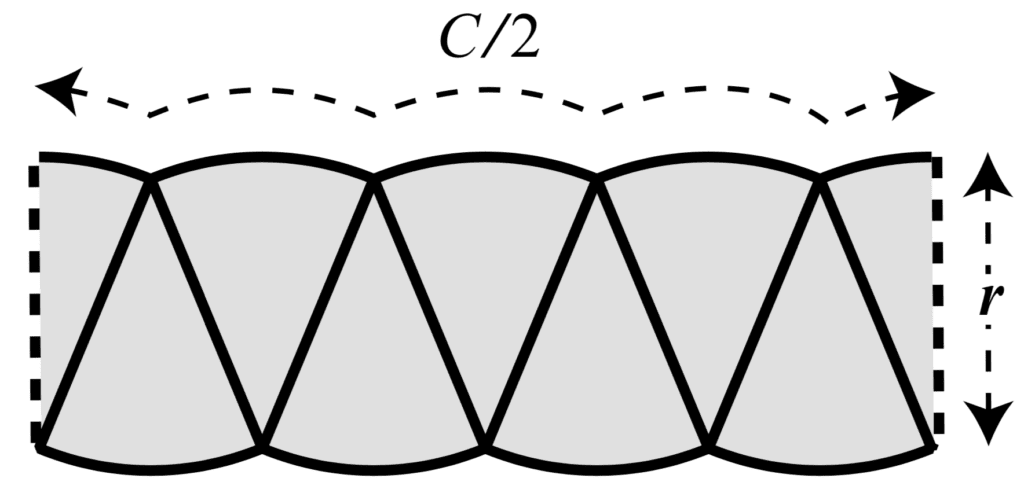
Réorganiser les tranches d’un cercle dans un rectangle
Tiré de Pouvoirs infinis.
Pour aplatir davantage la courbure, nous pouvons découper le cercle en morceaux plus minces.
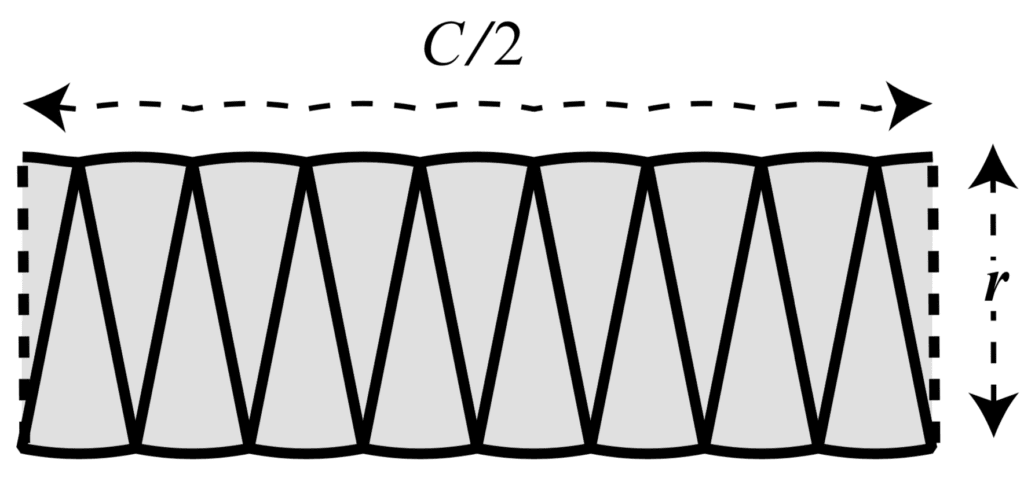
Réorganiser les tranches plus fines d’un cercle en un rectangle
Tiré de Pouvoirs infinis.
Plus les tranches sont fines, plus la courbure s’aplatit jusqu’à atteindre la limite de infiniment de nombreuses tranches, dont la forme est maintenant parfaitement rectangulaire.

Réorganiser des tranches infiniment fines d’un cercle en un rectangle
Tiré de Pouvoirs infinis.
Nous avons découpé les tranches dans la forme circulaire et les réorganiser en rectangle ne change pas leur surface. Par conséquent, calculer l’aire du cercle équivaut à calculer l’aire du rectangle résultant : UNE = RC/2.
Les courbes ne sont pas seulement une caractéristique des formes géométriques, mais apparaissent également dans la nature sous la forme d’arcs paraboliques tracés par des projectiles, ou les orbites elliptiques des planètes autour du soleil.
Et c’est ainsi qu’a commencé la deuxième grande obsession : une fascination pour les mystères du mouvement sur Terre et dans le système solaire.
– Page xix, Pouvoirs infinis, 2019.
Et avec les courbes et le mouvement, la prochaine question naturelle concerne leur taux de changement.
Les mystères des courbes et du mouvement étant désormais résolus, le calcul est passé à sa troisième obsession de longue date : le mystère du changement.
– Page xxii, Pouvoirs infinis, 2019.
C’est grâce à l’application du principe de l’infini que le calcul nous permet d’étudier le mouvement et le changement aussi, en les rapprochant en de nombreuses étapes infinitésimales.
C’est pour cette raison que le calcul est devenu le langage de l’univers.
Applications du calcul
Le calcul a été appliqué dans de nombreux domaines, de l’application de Newton à la résolution de problèmes de physique mathématique, à l’application plus récente des idées de Newton dans les travaux effectués à la NASA par la mathématicienne Katherine Johnson et ses collègues.
Dans les années 1860, James Clerk Maxwell a utilisé le calcul pour refondre les lois expérimentales de l’électricité et du magnétisme, prédisant finalement non seulement l’existence d’ondes électromagnétiques, mais révélant également la nature de la lumière en tant qu’onde électromagnétique. Sur la base de son travail, Nikola Tesla a créé le premier système de communication radio, Guglielmo Marconi a transmis les premiers messages sans fil, et finalement de nombreux appareils modernes, tels que la télévision et le smartphone, ont vu le jour.
Albert Einstein, en 1917, a également appliqué le calcul à un modèle de transitions atomiques, afin de prédire l’effet de l’émission stimulée. Son travail a ensuite conduit aux premiers lasers fonctionnels dans les années 1960, qui ont depuis lors été utilisés dans de nombreux appareils différents, tels que les lecteurs de disques compacts et les lecteurs de codes-barres.
Sans calcul, nous n’aurions pas de téléphones portables, d’ordinateurs ou de fours à micro-ondes. Nous n’aurions pas de radio. Ou la télévision. Ou échographie pour les femmes enceintes, ou GPS pour les voyageurs perdus. Nous n’aurions pas divisé l’atome, démêlé le génome humain ou envoyé des astronautes sur la lune. Nous n’avons peut-être même pas la déclaration d’indépendance.
– Page vii, Pouvoirs infinis, 2019.
Plus intéressant encore est le rôle intégral du calcul dans l’apprentissage automatique. Il sous-tend des algorithmes importants, tels que la descente de gradient, qui nécessite le calcul du gradient d’une fonction et est souvent essentiel pour entraîner des modèles d’apprentissage automatique. Cela fait du calcul l’un des outils mathématiques fondamentaux de l’apprentissage automatique.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Livres
Des articles
Résumé
Dans ce tutoriel, vous avez découvert les origines du calcul et ses applications.
Concrètement, vous avez appris :
- Ce calcul est l’étude mathématique du changement qui est basée sur une stratégie de coupe et de reconstruction.
- Ce calcul a permis de nombreuses découvertes et la création de nombreux appareils modernes tels que nous les connaissons, et constitue également un outil mathématique fondamental dans l’apprentissage automatique.
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.