[ad_1]
Dernière mise à jour le 19 juin 2021
La mesure du taux de changement est un concept intégral en calcul différentiel, qui concerne les mathématiques du changement et des infinitésimaux. Cela nous permet de trouver la relation entre deux variables changeantes et comment celles-ci s’affectent l’une l’autre.
La mesure du taux de changement est également essentielle pour l’apprentissage automatique, par exemple pour appliquer la descente de gradient comme algorithme d’optimisation pour entraîner un modèle de réseau neuronal.
Dans ce didacticiel, vous découvrirez le taux de changement comme l’un des concepts clés du calcul, et l’importance de le mesurer.
Après avoir terminé ce tutoriel, vous saurez :
- Comment le taux de changement des fonctions linéaires et non linéaires est mesuré.
- Pourquoi la mesure du taux de changement est un concept important dans différents domaines.
Commençons.

Concepts clés du calcul : taux de variation
Photo de Spencer Everett, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; elles sont:
- Taux de changement
- L’importance de mesurer le taux de changement
Taux de changement
Le taux de changement définit la relation d’une variable changeante par rapport à une autre.
Considérons un objet en mouvement qui se déplace deux fois plus dans la direction verticale, noté oui, car il est dans la direction horizontale, noté par X. En termes mathématiques, cela peut être exprimé par :
δoui = 2𝛿X
La lettre grecque delta, , est souvent utilisé pour désigner différence ou alors monnaie. Par conséquent, l’équation ci-dessus définit la relation entre le changement de la X-position par rapport à l’évolution de la oui-position de l’objet en mouvement.
Ce changement dans le X et oui-les directions peuvent être représentées par une ligne droite sur un X–oui coordonner système.
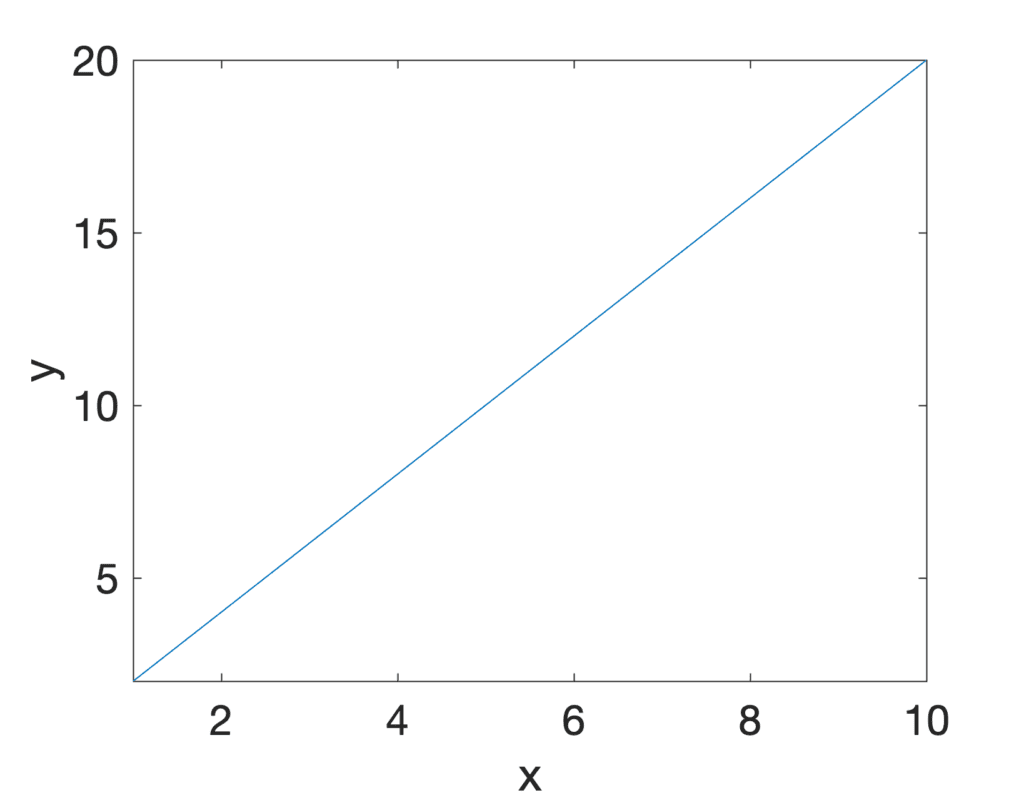
Tracé linéaire d’une fonction linéaire
Dans cette représentation graphique du mouvement de l’objet, le taux de changement est représenté par le pente de la ligne, ou son gradient. Puisque la ligne peut être vue se lever 2 unités pour chaque unité qu’il s’exécute vers la droite, alors son taux de variation, ou sa pente, est égal à 2.
Les tarifs et les pistes ont un lien simple. Les exemples de taux précédents peuvent être représentés graphiquement sur un système de coordonnées xy, où chaque taux apparaît sous la forme d’une pente.
Page 38, Calculus Essentials pour les nuls, 2019.
En liant tout ensemble, nous voyons que:
taux de variation =oui /X = montée / course = pente
Si nous devions considérer deux points particuliers, P1 = (2, 4) et P2 = (8, 16), sur cette droite, on peut confirmer que la pente est égale à :
pente =oui /X = (oui2 – oui1) / (X2 – X1) = (16 – 4) / (8 – 2) = 2
Pour cet exemple particulier, le taux de variation, représenté par la pente, est positif puisque la direction de la ligne augmente vers la droite. Cependant, le taux de variation peut également être négatif si la direction de la ligne diminue, ce qui signifie que la valeur de oui serait décroissant à mesure que la valeur de X augmente. De plus, lorsque la valeur de oui reste constant car X augmente, nous dirions que nous avons zéro taux de changement. Si, sinon, la valeur de X reste constant car oui augmente, nous considérerions que la plage de changement est infini, car la pente d’une ligne verticale est considérée comme indéfinie.
Jusqu’à présent, nous avons considéré l’exemple le plus simple d’avoir une ligne droite, et donc une fonction linéaire, avec une pente constante. Néanmoins, toutes les fonctions ne sont pas aussi simples, et si elles l’étaient, il n’y aurait pas besoin de calcul.
Le calcul est la mathématique du changement, c’est donc le bon moment pour passer aux paraboles, des courbes avec des pentes changeantes.
Page 39, Calculus Essentials pour les nuls, 2019.
Considérons une fonction non linéaire simple, une parabole :
oui = (1 / 4) X2
Contrairement à la pente constante qui caractérise une ligne droite, nous pouvons remarquer comment cette parabole devient de plus en plus raide au fur et à mesure que nous nous déplaçons vers la droite.
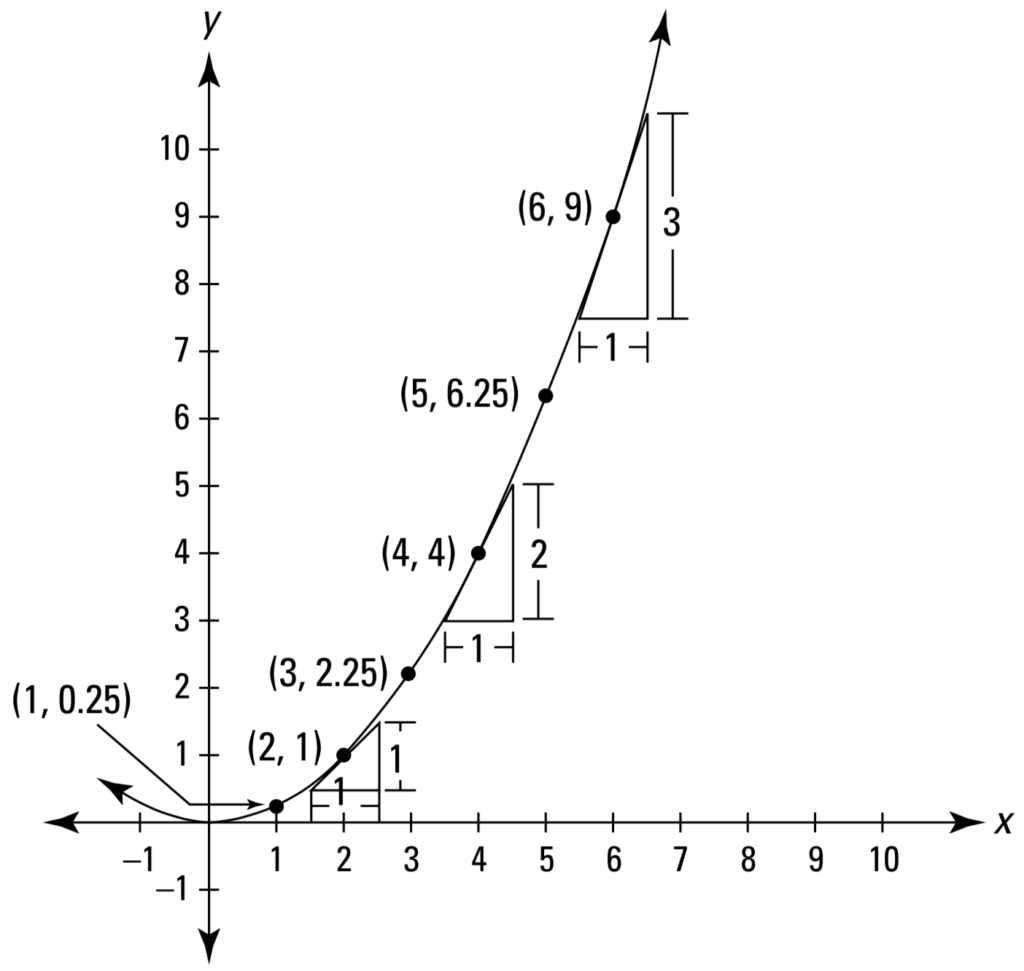
Tracé linéaire d’une parabole
Extrait de Calculus Essentials pour les nuls
Rappelons que la méthode du calcul permet d’analyser une forme courbe en la découpant en de nombreux morceaux droits infinitésimaux disposés les uns à côté des autres. Si nous devions considérer l’une de ces pièces à un moment donné, P, sur la forme courbe de la parabole, on voit qu’on se retrouve à recalculer le taux de variation comme la pente d’une droite. Il est important de garder à l’esprit que le taux de changement sur une parabole dépend du point particulier, P, que nous avons considéré en premier lieu.
Par exemple, si nous devions considérer la ligne droite qui passe par un point, P = (2, 1), nous trouvons que le taux de changement en ce point de la parabole est :
taux de variation =oui /X = 1 / 1 = 1
Si nous devions considérer un point différent sur la même parabole, à P = (6, 9), nous trouvons que le taux de variation à ce point est égal à :
taux de variation =oui /X = 3 / 1 = 3
La ligne droite qui touche la courbe comme un point particulier, P, est connu sous le nom de tangente ligne, alors que le processus de calcul du taux de changement d’une fonction est également connu comme la recherche de son dérivé.
Un dérivé est simplement une mesure de combien une chose change par rapport à une autre – et c’est un taux.
Page 37, Calculus Essentials pour les nuls, 2019.
Bien que nous ayons considéré une parabole simple pour cet exemple, nous pouvons également utiliser le calcul pour analyser des fonctions non linéaires plus compliquées. Le concept de calcul du taux de variation instantané à différents points tangentiels de la courbe reste le même.
Nous rencontrons un tel exemple lorsque nous arrivons à entraîner un réseau de neurones à l’aide de l’algorithme de descente de gradient. En tant qu’algorithme d’optimisation, la descente de gradient descend itérativement une fonction d’erreur vers son minimum global, mettant à chaque fois à jour les poids du réseau neuronal pour mieux modéliser les données d’apprentissage. La fonction d’erreur est, typiquement, non linéaire et peut contenir de nombreux minima locaux et points de selle. Afin de trouver son chemin en descente, l’algorithme de descente de gradient calcule la pente instantanée en différents points de la fonction d’erreur, jusqu’à ce qu’elle atteigne un point auquel l’erreur est la plus faible et le taux de variation est nul.
L’importance de mesurer le taux de changement
Jusqu’à présent, nous avons considéré le taux de variation par unité sur le X–oui système de coordonnées.
Mais un taux peut être n’importe quoi pour n’importe quoi.
Page 38, Calculus Essentials pour les nuls, 2019.
Dans le contexte de l’apprentissage d’un réseau de neurones, par exemple, nous avons vu que le gradient d’erreur est calculé comme le changement d’erreur par rapport à un poids spécifique dans le réseau de neurones.
Il existe de nombreux domaines différents dans lesquels la mesure du taux de changement est également un concept important. Voici quelques exemples :
- En physique, la vitesse est calculé comme le changement de position par unité de temps.
- Dans la numérisation du signal, taux d’échantillonnage est calculé comme le nombre d’échantillons de signal par seconde.
- En informatique, débit binaire est le nombre de bits traités par l’ordinateur par unité de temps.
- En finance, taux de change fait référence à la valeur d’une devise par rapport à une autre.
Dans les deux cas, chaque taux est un dérivé, et chaque dérivé est un taux.
Page 38, Calculus Essentials pour les nuls, 2019.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Livres
Résumé
Dans ce didacticiel, vous avez découvert le taux de changement comme l’un des concepts clés du calcul et l’importance de le mesurer.
Concrètement, vous avez appris :
- La mesure du taux de changement est un concept intégral du calcul différentiel qui nous permet de trouver la relation d’une variable changeante par rapport à une autre.
- Il s’agit d’un concept important qui peut être appliqué à de nombreux domaines, dont l’apprentissage automatique.
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.