Dernière mise à jour le 8 février 2022

Les dérivés sont l’un des concepts les plus fondamentaux du calcul. Ils décrivent comment les modifications des entrées variables affectent les sorties de la fonction. L’objectif de cet article est de fournir une introduction de haut niveau au calcul des dérivés dans PyTorch pour ceux qui découvrent le framework. PyTorch offre un moyen pratique de calculer les dérivées pour les fonctions définies par l’utilisateur.

Alors que nous devons toujours faire face à la rétropropagation (un algorithme connu pour être l’épine dorsale d’un réseau de neurones) dans les réseaux de neurones, qui optimise les paramètres pour minimiser l’erreur afin d’obtenir une plus grande précision de classification ; les concepts appris dans cet article seront utilisés dans des articles ultérieurs sur l’apprentissage en profondeur pour le traitement d’image et d’autres problèmes de vision par ordinateur.

Après avoir suivi ce didacticiel, vous apprendrez :

• Comment calculer les dérivées dans PyTorch.
• Comment utiliser autograd dans PyTorch pour effectuer une différenciation automatique sur les tenseurs.
• À propos du graphe de calcul qui implique différents nœuds et feuilles, vous permettant de calculer les gradients de la manière la plus simple possible (en utilisant la règle de la chaîne).
• Comment calculer les dérivées partielles dans PyTorch.
• Comment implémenter la dérivée de fonctions par rapport à plusieurs valeurs.

Commençons.

Différenciation dans Autograd

L’autograd – un module de différenciation automatique dans PyTorch – est utilisé pour calculer les dérivées et optimiser les paramètres dans les réseaux de neurones. Il est destiné principalement aux calculs de gradient.

Avant de commencer, chargeons quelques bibliothèques nécessaires que nous utiliserons dans ce didacticiel.

Maintenant, utilisons un simple tenseur et définissons le requires_grad paramètre à vrai. Cela nous permet d’effectuer une différenciation automatique et permet à PyTorch d’évaluer les dérivées en utilisant la valeur donnée qui, dans ce cas, est 3,0.

Nous utiliserons une équation simple $y=3x^2$ comme exemple et prendrons la dérivée par rapport à la variable x. Alors, créons un autre tenseur selon l’équation donnée. De plus, nous appliquerons une méthode soignée .backward sur la variable y qui forme un graphe acyclique stockant l’historique des calculs et évalue le résultat avec .grad pour la valeur donnée.

Comme vous pouvez le voir, nous avons obtenu une valeur de 18, ce qui est correct.

Graphe de calcul

PyTorch génère des dérivées en construisant un graphe inversé dans les coulisses, tandis que les tenseurs et les fonctions inversées sont les nœuds du graphe. Dans un graphe, PyTorch calcule la dérivée d’un tenseur selon qu’il s’agit d’une feuille ou non.

PyTorch n’évaluera pas la dérivée d’un tenseur si son attribut feuille est défini sur True. Nous n’entrerons pas dans les détails sur la création et l’utilisation du graphe inversé, car le but ici est de vous donner une connaissance de haut niveau de la façon dont PyTorch utilise le graphe pour calculer les dérivées.

Alors, vérifions comment les tenseurs x et y regarder en interne une fois qu’ils sont créés. Pour x:

et pour y:

Comme vous pouvez le voir, chaque tenseur s’est vu attribuer un ensemble particulier d’attributs.

le data l’attribut stocke les données du tenseur tandis que l’attribut grad_fn L’attribut indique le nœud dans le graphique. De même, le .grad L’attribut contient le résultat de la dérivée. Maintenant que vous avez appris quelques bases sur l’autograd et le graphe de calcul dans PyTorch, prenons une équation un peu plus compliquée $y=6x^2+2x+4$ et calculons la dérivée. La dérivée de l’équation est donnée par :

$$\frac{dy}{dx} = 12x+2$$

En évaluant la dérivée à $x = 3$,

$$\left.\frac{dy}{dx}\right\vert_{x=3} = 12\times 3+2 = 38$$

Voyons maintenant comment PyTorch fait cela,

La dérivée de l’équation est 38, ce qui est correct.

Implémentation des dérivées partielles de fonctions

PyTorch nous permet également de calculer des dérivées partielles de fonctions. Par exemple, si nous devons appliquer une dérivation partielle à la fonction suivante,

$$f(u,v) = u^3+v^2+4uv$$

Sa dérivée par rapport à $u$ est,

$$\frac{\partial f}{\partial u} = 3u^2 + 4v$$

De même, la dérivée par rapport à $v$ sera,

$$\frac{\partial f}{\partial v} = 2v + 4u$$

Maintenant, faisons-le à la manière de PyTorch, où $u = 3$ et $v = 4$.

Nous créerons u, v et f tenseurs et appliquer les .backward attribut sur f pour calculer la dérivée. Enfin, nous évaluerons la dérivée à l’aide de la .grad par rapport aux valeurs de u et v.

Dérivée de fonctions à valeurs multiples

Que se passe-t-il si nous avons une fonction à plusieurs valeurs et que nous devons calculer la dérivée par rapport à ses multiples valeurs ? Pour cela, nous utiliserons l’attribut sum pour (1) produire une fonction à valeur scalaire, puis (2) prendre la dérivée. Voici comment nous pouvons voir le graphique “fonction vs dérivée”:

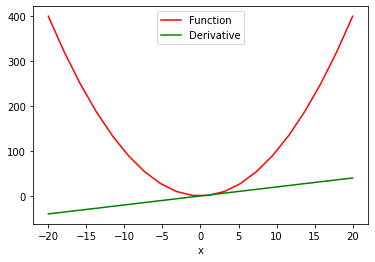
Dans les deux plot() fonction ci-dessus, nous extrayons les valeurs des tenseurs PyTorch afin de pouvoir les visualiser. le .detach La méthode ne permet pas au graphique de suivre davantage les opérations. Cela nous permet de convertir facilement un tenseur en un tableau numpy.

Résumé

Dans ce didacticiel, vous avez appris à implémenter des dérivées sur diverses fonctions dans PyTorch.

En particulier, vous avez appris :

• Comment calculer les dérivées dans PyTorch.
• Comment utiliser autograd dans PyTorch pour effectuer une différenciation automatique sur les tenseurs.
• À propos du graphe de calcul qui implique différents nœuds et feuilles, vous permettant de calculer les gradients de la manière la plus simple possible (en utilisant la règle de la chaîne).
• Comment calculer les dérivées partielles dans PyTorch.
• Comment implémenter la dérivée de fonctions par rapport à plusieurs valeurs.