[ad_1]
Dernière mise à jour le 2 mars 2022
Dans les langues, l’ordre des mots et leur position dans une phrase comptent vraiment. Le sens de la phrase entière peut changer si les mots sont réordonnés. Lors de la mise en œuvre de solutions NLP, les réseaux de neurones récurrents ont un mécanisme intégré qui traite de l’ordre des séquences. Le modèle de transformateur, cependant, n’utilise pas la récurrence ou la convolution et traite chaque point de données comme indépendant de l’autre. Par conséquent, les informations de position sont ajoutées au modèle explicitement pour conserver les informations concernant l’ordre des mots dans une phrase. Le codage positionnel est le schéma par lequel la connaissance de l’ordre des objets dans une séquence est maintenue.
Pour ce didacticiel, nous allons simplifier les notations utilisées dans cet article génial Attention is all You Need de Vaswani et al. Après avoir terminé ce didacticiel, vous saurez :
- Qu’est-ce que l’encodage positionnel et pourquoi est-ce important ?
- Codage de position dans les transformateurs
- Coder et visualiser une matrice d’encodage positionnel en Python à l’aide de NumPy
Commençons.

Une introduction en douceur au codage positionnel dans les modèles de transformateurs
Photo de Muhammad Murtaza Ghani sur Unsplash, certains droits réservés
Présentation du didacticiel
Ce tutoriel est divisé en quatre parties ; elles sont:
- Qu’est-ce que l’encodage positionnel
- Mathématiques derrière le codage positionnel dans les transformateurs
- Implémentation de la matrice d’encodage positionnel à l’aide de NumPy
- Comprendre et visualiser la matrice d’encodage positionnel
Qu’est-ce que l’encodage positionnel ?
Le codage positionnel décrit l’emplacement ou la position d’une entité dans une séquence de sorte que chaque position se voit attribuer une représentation unique. Il existe de nombreuses raisons pour lesquelles un nombre unique tel que la valeur d’index n’est pas utilisé pour représenter la position d’un élément dans les modèles de transformateur. Pour les longues séquences, les indices peuvent devenir importants. Si vous normalisez la valeur d’index entre 0 et 1, cela peut créer des problèmes pour les séquences de longueur variable car elles seraient normalisées différemment.
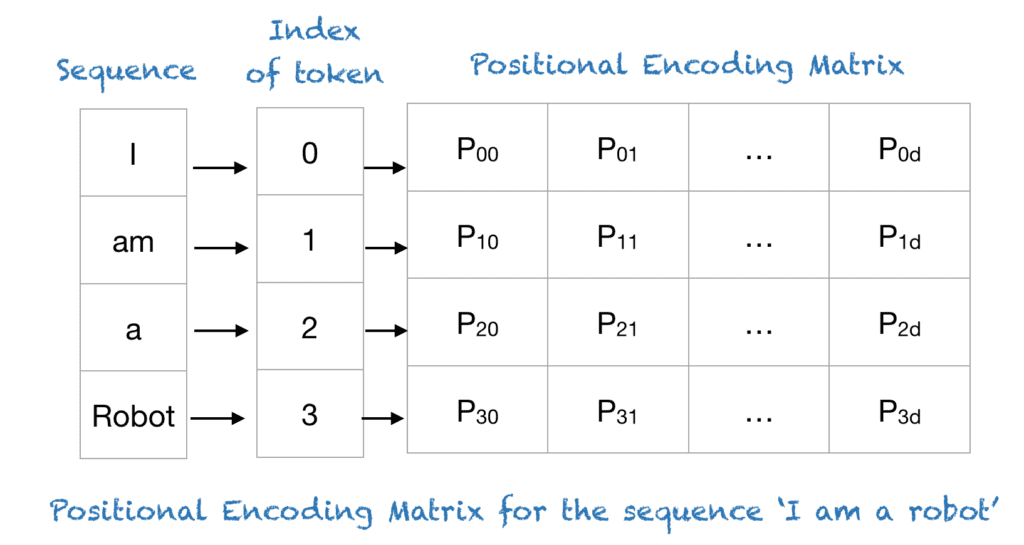
Les transformateurs utilisent un schéma de codage positionnel intelligent, où chaque position/index est mappé sur un vecteur. Par conséquent, la sortie de la couche de codage positionnel est une matrice, où chaque ligne de la matrice représente un objet codé de la séquence additionné avec ses informations de position. Un exemple de la matrice qui encode uniquement les informations de position est illustré dans la figure ci-dessous.
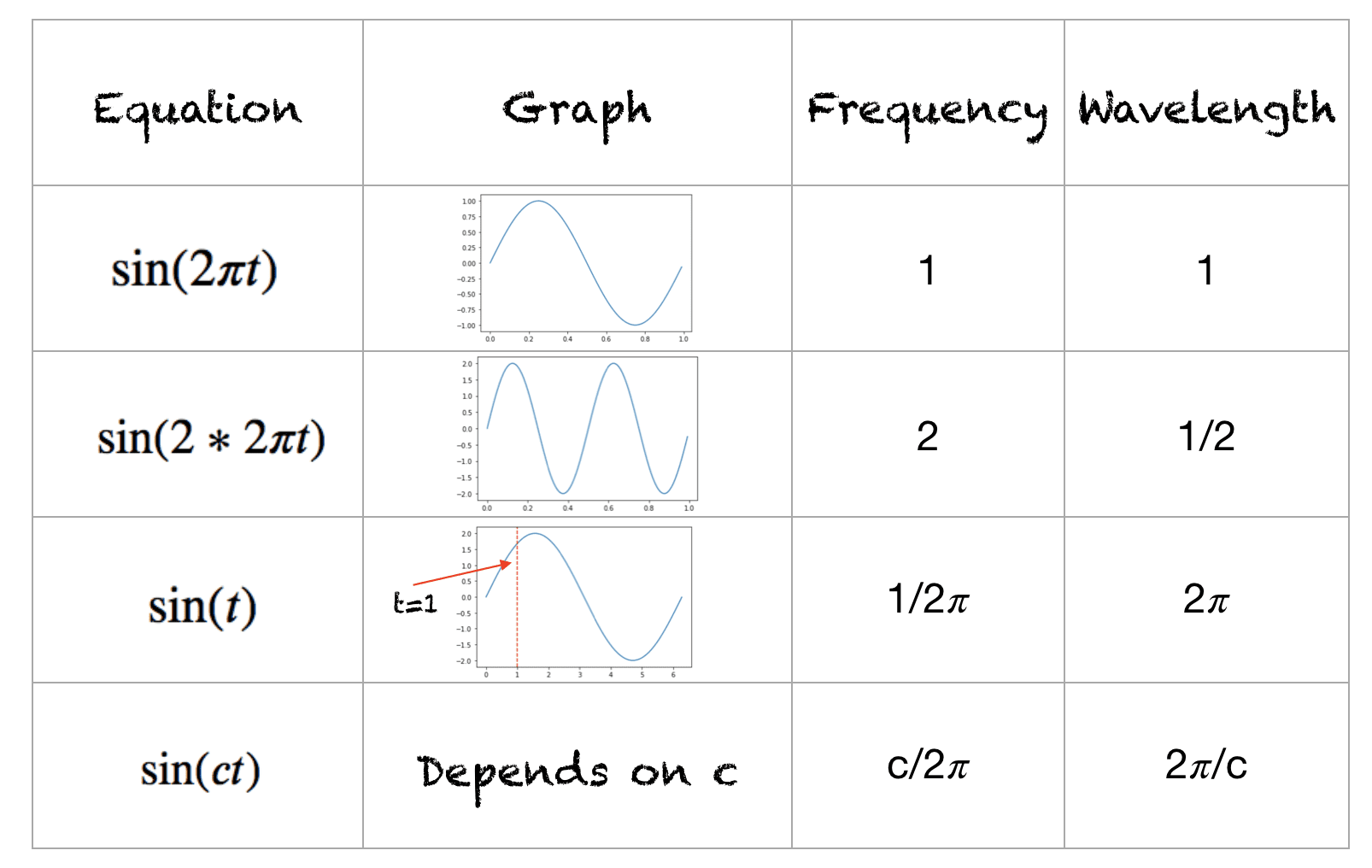
Une fonction sinusoïdale trigonométrique rapide
Ceci est un récapitulatif rapide des fonctions sinus et vous pouvez travailler de manière équivalente avec les fonctions cosinus. La plage de la fonction est [-1,+1]. La fréquence de cette forme d’onde est le nombre de cycles effectués en une seconde. La longueur d’onde est la distance sur laquelle la forme d’onde se répète. La longueur d’onde et la fréquence des différentes formes d’onde sont indiquées ci-dessous :
Couche de codage positionnel dans les transformateurs
Plongeons directement là-dedans. Supposons que nous ayons une séquence d’entrée de longueur $L$ et que nous ayons besoin de la position de l’objet $k^{th}$ dans cette séquence. Le codage positionnel est donné par des fonctions sinus et cosinus de fréquences variables :
\begin{eqnarray}
P(k, 2i) &=& \sin\Big(\frac{k}{n^{2i/d}}\Big)\\
P(k, 2i+1) &=& \cos\Big(\frac{k}{n^{2i/d}}\Big)
\end{eqnarray}
Ici:
$k$ : Position d’un objet dans la séquence d’entrée, $0 \leq k < L/2$
$d$ : Dimension de l’espace d’intégration de sortie
$P(k, j)$ : fonction de position pour mapper une position $k$ dans la séquence d’entrée à l’index $(k,j)$ de la matrice positionnelle
$n$ : scalaire défini par l’utilisateur. Fixé à 10 000 par les auteurs de Attention is all You Need.
$i$ : utilisé pour le mappage aux indices de colonne $0 \leq i < d/2$. Une seule valeur de $i$ correspond aux fonctions sinus et cosinus
Dans l’expression ci-dessus, nous pouvons voir que les positions paires correspondent à la fonction sinus et les positions impaires correspondent aux positions paires.
Exemple
Pour comprendre l’expression ci-dessus, prenons un exemple de la phrase “Je suis un robot”, avec n=100 et d=4. Le tableau suivant montre la matrice de codage positionnel pour cette phrase. En fait, la matrice de codage positionnel serait la même pour toute phrase de 4 lettres avec n = 100 et d = 4.

Codage de la matrice de codage positionnel à partir de zéro
Voici un court code Python pour implémenter l’encodage positionnel à l’aide de NumPy. Le code est simplifié pour faciliter la compréhension du codage positionnel.
|
importer numpy comme np importer matplotlib.pyplot comme plt définitivement getPositionEncoding(seq_len, ré, n=10000): P = np.des zéros((seq_len, ré)) pour k dans intervalle(seq_len): pour je dans np.arranger(entier(ré/2)): dénominateur = np.Puissance(n, 2*je/ré) P[k, 2*i] = np.péché(k/dénominateur) P[k, 2*i+1] = np.parce que(k/dénominateur) retourner P P = getPositionEncoding(seq_len=4, ré=4, n=100) impression(P) |
|
[[ 0. 1. 0. 1. ] [ 0.84147098 0.54030231 0.09983342 0.99500417] [ 0.90929743 -0.41614684 0.19866933 0.98006658] [ 0.14112001 -0.9899925 0.29552021 0.95533649]] |
Comprendre la matrice de codage positionnel
Pour comprendre le codage positionnel, commençons par regarder l’onde sinusoïdale pour différentes positions avec n = 10 000 et d = 512.
|
définitivement plotSinusoïde(k, ré=512, n=10000): X = np.arranger(0, 100, 1) dénominateur = np.Puissance(n, 2*X/ré) y = np.péché(k/dénominateur) plt.parcelle(X, y) plt.Titre(‘k = ‘ + chaîne(k)) figure = plt.chiffre(taille de figue=(15, 4)) pour je dans intervalle(4): plt.sous-parcelle(141 + je) plotSinusoïde(je*4) |
La figure suivante est la sortie du code ci-dessus :

Onde sinusoïdale pour différents indices de position
Nous pouvons voir que chaque position $k$ correspond à une sinusoïde différente, qui encode une seule position dans un vecteur. Si nous examinons de près la fonction de codage positionnel, nous pouvons voir que la longueur d’onde pour un $i$ fixe est donnée par :
$$
\lambda_{i} = 2 \pi n^{2i/d}
$$
Ainsi, les longueurs d’onde des sinusoïdes forment une progression géométrique et varient de $2\pi$ à $2\pi n$. Le schéma de codage positionnel présente un certain nombre d’avantages.
- Les fonctions sinus et cosinus ont des valeurs dans [-1, 1]qui conserve les valeurs de la matrice de codage positionnel dans une plage normalisée.
- Comme la sinusoïde de chaque position est différente, nous avons une manière unique d’encoder chaque position.
- Nous avons un moyen de mesurer ou de quantifier la similarité entre différentes positions, nous permettant ainsi d’encoder les positions relatives des mots.
Visualisation de la matrice positionnelle
Visualisons la matrice positionnelle sur des valeurs plus grandes. Nous utiliserons Python matshow() méthode de la matplotlib bibliothèque. En fixant n = 10 000 comme dans l’article original, nous obtenons ce qui suit :
|
P = getPositionEncoding(seq_len=100, ré=512, n=10000) encaisser = plt.matshow(P) plt.gcf().barre de couleur(encaisser) |
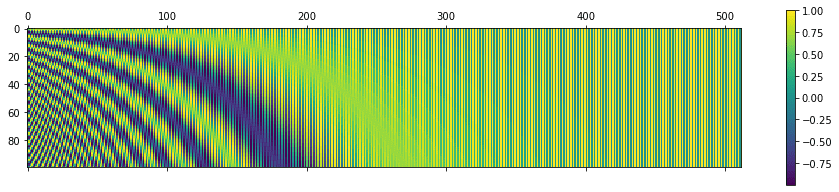
La matrice de codage positionnel pour n = 10 000, d = 512, longueur de séquence = 100
Quelle est la sortie finale de la couche d’encodage positionnel ?
La couche de codage positionnel additionne le vecteur positionnel avec le codage de mot et sort cette matrice pour les couches suivantes. L’ensemble du processus est illustré ci-dessous.
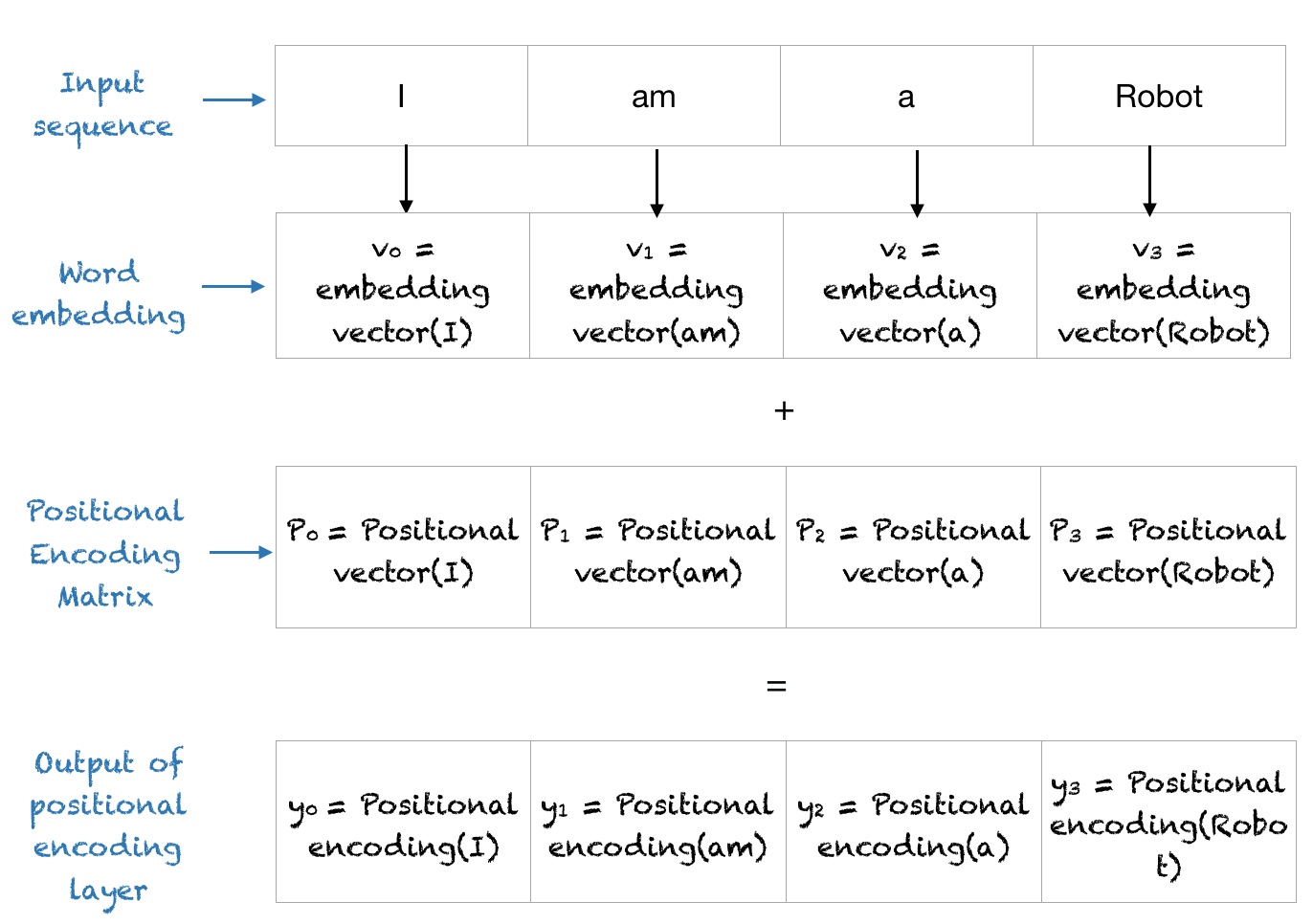
La couche de codage de position dans le transformateur
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Livres
Papiers
Des articles
Sommaire
Dans ce didacticiel, vous avez découvert l’encodage positionnel dans les transformateurs.
Plus précisément, vous avez appris :
- Qu’est-ce que l’encodage positionnel et pourquoi est-il nécessaire.
- Comment implémenter l’encodage positionnel en Python à l’aide de NumPy
- Comment visualiser la matrice d’encodage positionnel
Avez-vous des questions sur l’encodage positionnel abordé dans cet article ? Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.