[ad_1]
La procédure de descente de gradient est une méthode qui revêt une importance primordiale dans l’apprentissage automatique. Il est souvent utilisé pour minimiser les fonctions d’erreur dans les problèmes de classification et de régression. Il est également utilisé dans la formation de réseaux de neurones et d’architectures d’apprentissage en profondeur.
Dans ce tutoriel, vous découvrirez la procédure de descente de gradient.
Après avoir terminé ce tutoriel, vous saurez :
- Méthode de descente en dégradé
- Importance de la descente de gradient dans l’apprentissage automatique
Commençons.

Une introduction douce à la descente de pente. Photo de Mehreen Saeed, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; ils sont:
- Procédure de descente de gradient
- Exemple de procédure de descente de pente résolu
Conditions préalables
Pour ce didacticiel, la connaissance préalable des sujets suivants est supposée :
Vous pouvez revoir ces concepts en cliquant sur le lien ci-dessus.
Procédure de descente de gradient
La procédure de descente de gradient est un algorithme pour trouver le minimum d’une fonction.
Supposons que nous ayons une fonction f(x), où x est un tuple de plusieurs variables, c’est-à-dire x = (x_1, x_2, …x_n). Supposons également que le gradient de f(x) soit donné par ∇f(x). On veut trouver la valeur des variables (x_1, x_2, …x_n) qui nous donnent le minimum de la fonction. À toute itération t, nous noterons la valeur du tuple x par x[t]. Donc x[t][1] est la valeur de x_1 à l’itération t, x[t][2] est la valeur de x_2 à l’itération t, etc.
La notation
Nous avons les variables suivantes :
- t = numéro d’itération
- T = nombre total d’itérations
- n = Total des variables dans le domaine de f (également appelé dimensionnalité de x)
- j = Itérateur pour le numéro de variable, par exemple, x_j représente la jième variable
- 𝜂 = Taux d’apprentissage
- f(x[t]) = Valeur du vecteur gradient de f à l’itération t
La méthode de formation
Les étapes de l’algorithme de descente de gradient sont indiquées ci-dessous. C’est ce qu’on appelle aussi la méthode d’entraînement.
- Choisissez un point initial aléatoire x_initial et définissez x[0] = x_initial
- Pour les itérations t=1..T
- Mettre à jour x[t] = x[t-1] – f(x[t-1])
C’est aussi simple que ça!
Le taux d’apprentissage est une variable définie par l’utilisateur pour la procédure de descente de gradient. Sa valeur se situe dans la plage [0,1].
La méthode ci-dessus dit qu’à chaque itération, nous devons mettre à jour la valeur de x en faisant un petit pas dans la direction du négatif du vecteur gradient. Si 𝜂=0, alors il n’y aura pas de changement dans x. Si 𝜂=1, alors c’est comme faire un grand pas dans la direction du négatif du gradient du vecteur. Normalement, est défini sur une petite valeur comme 0,05 ou 0,1. Il peut également être variable au cours de la procédure d’entraînement. Ainsi, votre algorithme peut commencer par une grande valeur (par exemple 0,8) puis le réduire à des valeurs plus petites.
Exemple de descente de gradient
Trouvons le minimum de la fonction suivante de deux variables, dont les graphiques et les contours sont représentés dans la figure ci-dessous :
f(x,y) = x*x + 2y*oui

Graphique et contours de f(x,y) = x*x + 2y*y
La forme générale du vecteur gradient est donnée par :
f(x,y) = 2xi + 4yj
Deux itérations de l’algorithme, T=2 et =0.1 sont présentées ci-dessous
- t initial=0
- X[0] = (4,3) # Ceci est juste un point choisi au hasard
- À t = 1
- X[1] = x[0] – f(x[0])
- X[1] = (4,3) – 0,1*(8,12)
- X[1] = (3.2,1.8)
- À t=2
- X[2] = x[1] – f(x[1])
- X[2] = (3,2, 1,8) – 0,1* (6,4, 7,2)
- X[2] = (2.56,1.08)
Si vous continuez à exécuter les itérations ci-dessus, la procédure finira par se terminer au point où la fonction est minimale, c’est-à-dire (0,0).
A l’itération t=1, l’algorithme est illustré dans la figure ci-dessous :
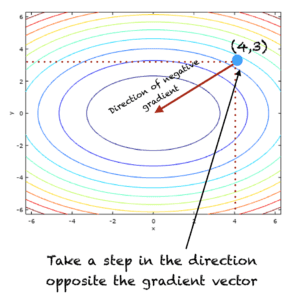
Illustration de la procédure de descente en pente
Combien d’itérations exécuter ?
Normalement, la descente de gradient est exécutée jusqu’à ce que la valeur de x ne change pas ou que le changement de x soit inférieur à un certain seuil. Le critère d’arrêt peut également être un nombre maximum d’itérations défini par l’utilisateur (que nous avons défini précédemment comme T).
Ajouter de l’élan
La descente de gradient peut rencontrer des problèmes tels que :
- Osciller entre deux ou plusieurs points
- Se faire piéger dans un minimum local
- Dépasser et manquer le point minimum
Pour résoudre les problèmes ci-dessus, un terme de quantité de mouvement peut être ajouté à l’équation de mise à jour de l’algorithme de descente de gradient comme suit :
X[t] = x[t-1] – f(x[t-1]) + *Δx[t-1]
où x[t-1] représente la variation de x, c’est-à-dire
x[t] = x[t] – X[t-1]
Le changement initial à t=0 est un vecteur nul. Pour ce problème Δx[0] = (0,0).
À propos de la montée en dégradé
Il existe une procédure de montée de gradient connexe, qui trouve le maximum d’une fonction. En descente de gradient, nous suivons la direction du taux de décroissance maximale d’une fonction. C’est la direction du vecteur gradient négatif. Alors que, dans la montée en gradient, nous suivons la direction du taux d’augmentation maximal d’une fonction, qui est la direction pointée par le vecteur gradient positif. Nous pouvons également écrire un problème de maximisation en termes de problème de maximisation en ajoutant un signe négatif à f(x), c’est-à-dire,
|
maximiser F(X) w.r.t X est équivalent à minimiser –F(X) w.r.t X |
Pourquoi la descente de gradient est-elle importante dans l’apprentissage automatique ?
L’algorithme de descente de gradient est souvent utilisé dans les problèmes d’apprentissage automatique. Dans de nombreuses tâches de classification et de régression, la fonction d’erreur quadratique moyenne est utilisée pour ajuster un modèle aux données. La procédure de descente de gradient est utilisée pour identifier les paramètres de modèle optimaux qui conduisent à l’erreur quadratique moyenne la plus faible.
L’ascension du gradient est utilisée de la même manière, pour les problèmes impliquant la maximisation d’une fonction.
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Thomas’ Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Résumé
Dans ce tutoriel, vous avez découvert l’algorithme de descente de gradient. Concrètement, vous avez appris :
- Procédure de descente de gradient
- Comment appliquer la procédure de descente de gradient pour trouver le minimum d’une fonction
- Comment transformer un problème de maximisation en problème de minimisation
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.