[ad_1]
Des formes indéterminées sont souvent rencontrées lors de l’évaluation des limites des fonctions, et les limites jouent à leur tour un rôle important en mathématiques et en calcul. Ils sont essentiels pour en savoir plus sur les dérivés, les dégradés, les jutes et bien plus encore.
Dans ce tutoriel, vous découvrirez comment évaluer les limites des formes indéterminées et la règle de L’Hospital pour les résoudre.
Après avoir terminé ce tutoriel, vous saurez :
- Comment évaluer les limites des fonctions de types indéterminés de la forme 0/0 et ∞/∞
- La règle de L’Hospital pour évaluer les types indéterminés
- Comment convertir des types indéterminés plus complexes et leur appliquer la règle de L’Hospital
Commençons.

Une introduction douce aux formes indéterminées et à la règle de L’Hospital Photo de Mehreen Saeed, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en 2 parties ; ils sont:
- Les formes indéterminées de type 0/0 et ∞/∞
- Comment appliquer la règle de L’Hospital à ces types
- Exemples résolus de ces deux types indéterminés
- Types indéterminés plus complexes
- Comment convertir les types indéterminés les plus complexes en formes 0/0 et ∞/∞
- Exemples résolus de ces types
Conditions préalables
Ce didacticiel nécessite une compréhension de base des deux sujets suivants :
Si vous n’êtes pas familier avec ces sujets, vous pouvez les consulter en cliquant sur les liens ci-dessus.
Que sont les formes indéterminées ?
Lors de l’évaluation des limites, nous rencontrons des situations où les règles de base pour l’évaluation des limites peuvent échouer. Par exemple, nous pouvons appliquer la règle du quotient dans le cas de fonctions rationnelles :
lim(x→a) f(x)/g(x) = (lim(x→a)f(x))/(lim(x→a)g(x)) si lim(x→a)g( x)≠0
La règle ci-dessus ne peut être appliquée que si l’expression au dénominateur ne s’approche pas de zéro lorsque x s’approche de a. Une situation plus compliquée se présente si le numérateur et le dénominateur s’approchent tous les deux de zéro lorsque x s’approche de a. C’est ce qu’on appelle une forme indéterminée de type 0/0. De même, il existe des formes indéterminées du type ∞/∞, données par :
lim(x→a) f(x)/g(x) = (lim(x→a)f(x))/(lim(x→a)g(x)) quand lim(x→a)f( x)=∞ et lim(x→a)g(x)=∞
Quelle est la règle de L’Hospital ?
Le règlement de L’Hospital stipule ce qui suit :

La règle de L’Hospital
Quand appliquer la règle de L’Hospital
Un point important à noter est que la règle de L’Hospital n’est applicable que lorsque les conditions pour f(x) et g(x) sont remplies. Par exemple:
- lim(𝑥→0) sin(x)/(x+1) Ne peut pas appliquer la règle de L’Hospital car ce n’est pas la forme 0/0
- lim(𝑥→0) sin(x)/x Peut appliquer la règle sous sa forme 0/0
- lim(𝑥→∞) (e^x)/(1/x+1) Ne peut pas appliquer la règle de L’Hospital car ce n’est pas la forme ∞/∞
- lim(𝑥→∞) (e^x)/x Peut appliquer la règle de L’Hospital sous la forme ∞/∞
Exemples de 0/0 et ∞/∞
Quelques exemples de ces deux types et comment les résoudre sont présentés ci-dessous. Vous pouvez également vous référer à la figure ci-dessous pour faire référence à ces fonctions.
Exemple 1.1 : 0/0
Evaluer lim(𝑥→2) ln(x-1)/(x-2) (Voir le graphique de gauche sur la figure)
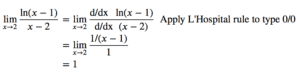
lim(𝑥→2) ln(x-1)/(x-2)=1
Exemple 1.2 : ∞/∞
Évaluer lim(𝑥→∞) ln(x)/x (Voir le graphique de droite sur la figure)

lim(𝑥→∞) ln(x)/x=0

Graphiques des exemples 1.1 et 1.2
Plus de formes indéterminées
La règle de L’Hospital ne nous dit que comment traiter les formes 0/0 ou ∞/∞. Cependant, il existe des formes plus indéterminées qui impliquent des produits, des différences et des pouvoirs. Alors comment gérer le reste ? Nous pouvons utiliser des astuces mathématiques astucieuses pour convertir des produits, des différences et des puissances en quotients. Cela peut nous permettre d’appliquer facilement la règle de L’Hospital à presque toutes les formes indéterminées. Le tableau ci-dessous présente différentes formes indéterminées et comment les traiter.

Comment résoudre des formes indéterminées plus complexes
Exemples
Les exemples suivants montrent comment vous pouvez convertir une forme indéterminée en forme 0/0 ou ∞/∞ et appliquer la règle de L’Hospital pour résoudre la limite. Après les exemples élaborés, vous pouvez également consulter les graphiques de toutes les fonctions dont les limites sont calculées.
Exemple 2.1 : 0.∞
Évaluer lim(𝑥→∞) x.sin(1/x) (Voir le premier graphique de la figure)
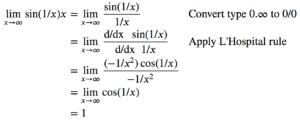
lim(𝑥→∞) x.sin(1/x)=1
Exemple 2.2 : ∞-∞
Évaluer lim(𝑥→0) 1/(1-cos(x)) – 1/x (Voir le deuxième graphique de la figure ci-dessous)
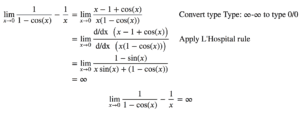
lim(𝑥→0) 1/(1-cos(x)) – 1/x =∞
Exemple 2.3 : Forme de puissance
Évaluer lim(𝑥→∞) (1+x)^(1/x) (Voir le troisième graphique de la figure ci-dessous)

lim(𝑥→∞) (1+x)^(1/x)=1
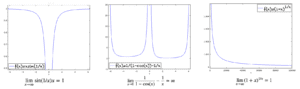
Graphiques des exemples 2.1, 2.2 et 2.3
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
- Théorème de la valeur moyenne de Cauchy
- Le théorème de Rolle
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Thomas’ Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Résumé
Dans ce tutoriel, vous avez découvert le concept de formes indéterminées et comment les évaluer.
Concrètement, vous avez appris :
- Formes indéterminées de type 0/0 et ∞/∞
- Règle de L’Hospital pour évaluer les types 0/0 et ∞/∞
- Formes indéterminées de type 0.∞, ∞-∞ et formes de puissance, et comment les évaluer.
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.