Dernière mise à jour le 9 juillet 2021

L’optimisation, en tant que l’un des processus centraux de nombreux algorithmes d’apprentissage automatique, repose sur l’utilisation de dérivés afin de décider de quelle manière mettre à jour les valeurs des paramètres d’un modèle, pour maximiser ou minimiser une fonction objectif.

Ce tutoriel continuera à explorer les différentes techniques par lesquelles nous pouvons trouver les dérivées de fonctions. En particulier, nous explorerons les règles de puissance, de produit et de quotient, que nous pouvons utiliser pour arriver aux dérivées des fonctions plus rapidement que si nous devions trouver toutes les dérivées à partir des principes premiers. Par conséquent, pour les fonctions particulièrement difficiles, garder ces règles à portée de main pour trouver leurs dérivées deviendra de plus en plus important.

Dans ce tutoriel, vous découvrirez les règles de puissance, de produit et de quotient pour trouver la dérivée des fonctions.

Après avoir terminé ce tutoriel, vous saurez :

• La règle de puissance à suivre pour trouver la dérivée d’une base variable, élevée à une puissance fixe.
• Comment la règle du produit nous permet de trouver la dérivée d’une fonction définie comme le produit de deux autres fonctions (ou plus).
• Comment la règle du quotient nous permet de trouver la dérivée d’une fonction qui est le rapport de deux fonctions dérivables.

Commençons.

Présentation du didacticiel

Ce tutoriel est divisé en trois parties ; ils sont:

• La règle du pouvoir
• La règle du produit
• La règle du quotient

La règle du pouvoir

Si on a une base variable élevée à une puissance fixe, la règle à suivre pour trouver sa dérivée est de faire baisser la puissance devant la base variable, puis de soustraire la puissance par 1.

Par exemple, si nous avons la fonction, F(X) = X², dont on voudrait trouver la dérivée, on abaisse d’abord 2 devant X puis réduisez la puissance de 1 :

F(X) = X²

F‘(X) = 2X

Afin de mieux comprendre d’où vient cette règle, prenons le chemin le plus long et trouvons la dérivée de F(X) en partant de la définition d’une dérivée :

Ici, on remplace F(X) = X² puis procéder à la simplification de l’expression :

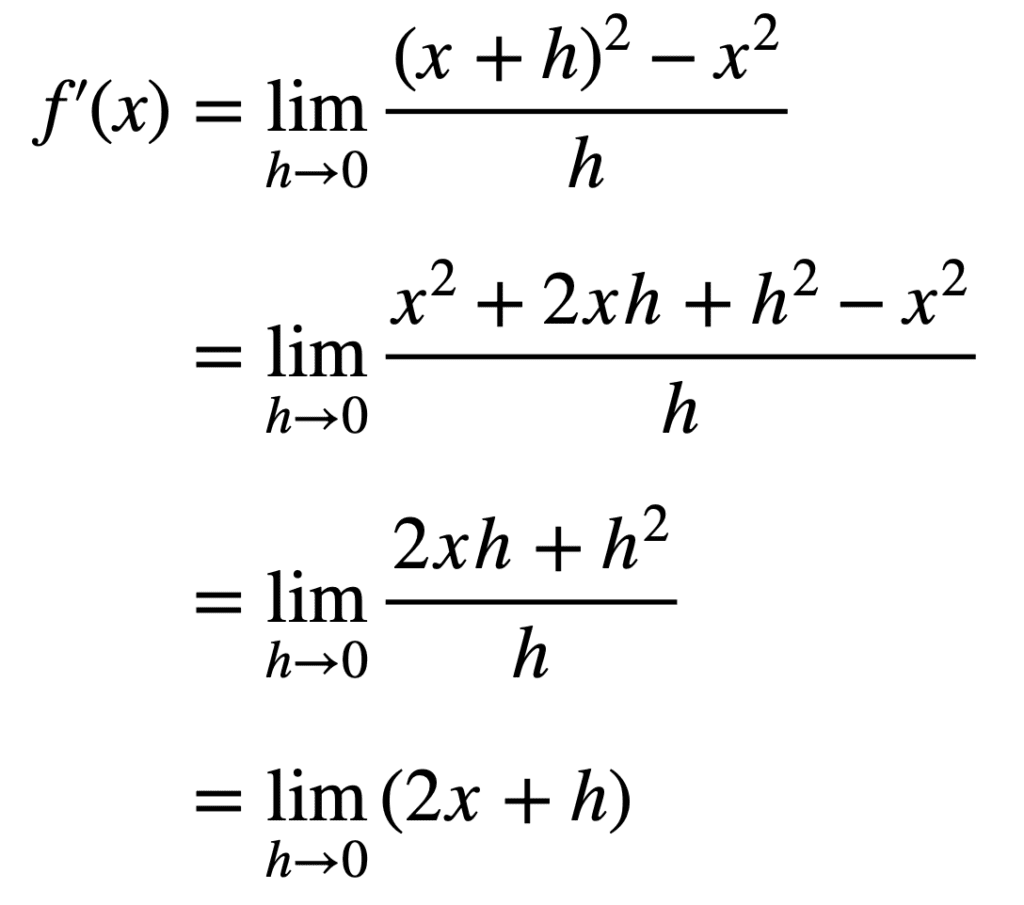
Comme h s’approche d’une valeur de 0, alors cette limite s’approche de 2X, ce qui correspond au résultat que nous avons obtenu précédemment en utilisant la règle de puissance.

Si appliqué à F(X) = X, la règle de puissance nous donne une valeur de 1. C’est parce que, lorsque nous amenons une valeur de 1 devant X, puis soustrayez la puissance de 1, il nous reste une valeur de 0 dans l’exposant. Depuis, X⁰ = 1, alors F‘(X) = (1) (X⁰)= 1.

La meilleure façon de comprendre cette dérivée est de réaliser que f(x) = x est une droite qui correspond à la forme y = mx + b parce que f(x) = x est la même chose que f(x) = 1x + 0 (ou y = 1x + 0). La pente (m) de cette droite est 1, donc la dérivée est égale à 1. Ou vous pouvez simplement mémoriser que la dérivée de x est 1. Mais si vous oubliez ces deux idées, vous pouvez toujours utiliser la règle de puissance.

Page 131, Calcul pour les nuls, 2016.

La règle de puissance peut être appliquée à n’importe quelle puissance, qu’elle soit positive, négative ou fractionnaire. Nous pouvons également l’appliquer aux fonctions radicales en exprimant d’abord leur exposant (ou puissance) sous forme de fraction :

F(X) =X = X^1/2

F’(X) = (1 / 2) X^-1/2

La règle du produit

Supposons que nous ayons maintenant une fonction, F(X), dont nous aimerions trouver la dérivée, qui est le produit de deux autres fonctions, vous(X) = 2X² et v(X) = X³:

F(X) = vous(X) v(X) = (2X²) (X³)

Afin d’étudier comment s’y prendre pour trouver la dérivée de F(X), commençons par trouver la dérivée du produit de vous(X) et v(X) directement :

(vous(X) v(X))’ = ((2X²) (X³))’ = (2X⁵)’ = 10X⁴

Examinons maintenant ce qui se passe si, sinon, nous devons d’abord calculer les dérivées des fonctions séparément, puis les multiplier ensuite :

vous(X) v’(X) = (2X²)’ (X³)’ = (4X) (3X²) = 12X³

Il est clair que le deuxième résultat ne concorde pas avec le premier, et c’est parce que nous n’avons pas appliqué le Règle du produit.

La règle du produit nous dit que la dérivée du produit de deux fonctions peut être trouvée comme :

F’(X) = vous(X) v(X) + vous(X) v’(X)

On peut arriver à la règle du produit si on avance en appliquant les propriétés des limites, en repartant de la définition d’une dérivée :

Nous savons que F(X) = vous(X) v(X) et, par conséquent, nous pouvons remplacer F(X) et F(X + h):

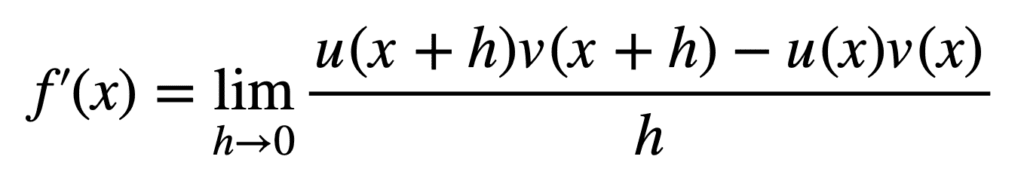
A ce stade, notre objectif est de factoriser le numérateur en plusieurs limites qui peuvent ensuite être évaluées séparément. A cet effet, la soustraction de termes, vous(X) v(x + h) – vous(X) v(x + h), doit être introduit dans le numérateur. Son introduction ne modifie pas la définition de F‘(X) que nous venons d’obtenir, mais cela nous aidera à factoriser le numérateur :

L’expression résultante semble compliquée, cependant, si nous regardons de plus près, nous nous rendons compte que nous avons des termes communs qui peuvent être factorisés :

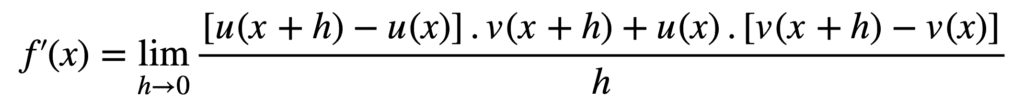
L’expression peut être encore simplifiée en appliquant les lois limites qui permettent de séparer les sommes et les produits en limites distinctes :

La solution à notre problème est maintenant devenue plus claire. On voit que les premier et dernier termes de l’expression simplifiée correspondent à la définition de la dérivée de vous(X) et v(X), que l’on peut désigner par vous(X)’ et v(X)’, respectivement. Le second terme se rapproche de la fonction continue et dérivable, v(X), comme h se rapproche de 0, alors que le troisième terme est vous(X).

Par conséquent, nous arrivons à nouveau à la règle du produit :

F’(X) = vous(X) v(X) + vous(X) v’(X)

Avec ce nouvel outil en main, reconsidérons la recherche F‘(X) lorsque vous(X) = 2X² et v(X) = X³:

F’(X) = vous(X) v(X) + vous(X) v’(X)

F’(X) = (4X) (X³) + (2X²) (3X²) = 4X⁴ + 6X⁴ = 10X⁴

La dérivée résultante correspond maintenant correctement à la dérivée du produit, (vous(X) v(X))’, que nous avons obtenu précédemment.

C’était un exemple assez simple que nous aurions pu calculer directement en premier lieu. Cependant, nous pourrions avoir des problèmes plus complexes impliquant des fonctions qui ne peuvent pas être multipliées directement, auxquelles nous pouvons facilement appliquer la règle du produit. Par exemple:

F(X) = X² péché X

F’(X) = (X²)’ (péché X) + (X²) (péché X)’ = 2X péché X + X² car X

On peut même étendre la règle du produit à plus de deux fonctions. Par exemple, disons F(X) est maintenant défini comme le produit de trois fonctions, vous(X), v(X) et w(X):

F(X) = vous(X) v(X) w(X)

Nous pouvons appliquer la règle du produit comme suit :

F‘(X) = vous‘(X) v(X) w(X) + vous(X) v‘(X) w(X) + vous(X) v(X) w‘(X)

La règle du quotient

De même, la règle du quotient nous dit comment trouver la dérivée d’une fonction, F(X), c’est-à-dire le rapport de deux fonctions différentiables, vous(X) et v(X):

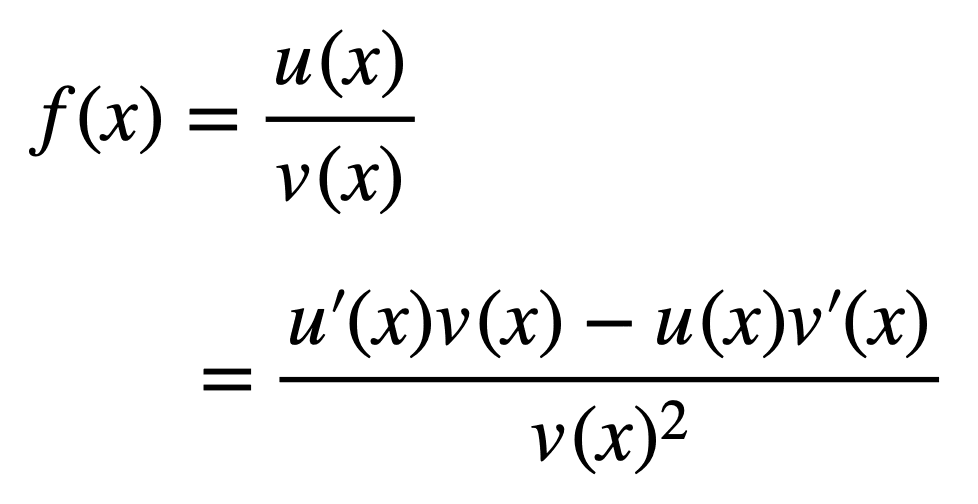
On peut dériver la règle du quotient des premiers principes comme on l’a fait pour la règle du produit, c’est-à-dire en partant de la définition d’une dérivée et en appliquant les propriétés des limites. Ou nous pouvons prendre un raccourci et dériver la règle du quotient en utilisant la règle du produit elle-même. Prenons cette route cette fois-ci :

Nous pouvons appliquer la règle du produit sur vous(X) obtenir:

vous‘(X) = F‘(X) v(X) + F(X) v‘(X)

Résoudre pour F‘(X) nous donne:

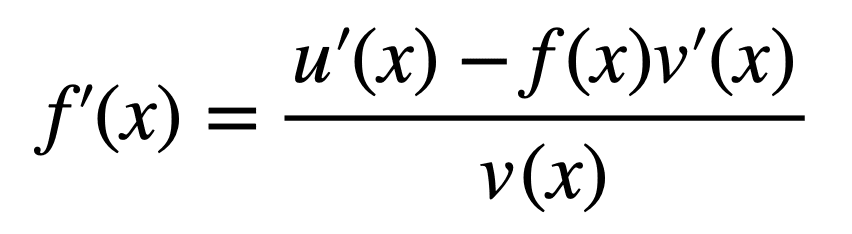
Une dernière étape remplace F(X) pour arriver à la règle du quotient :

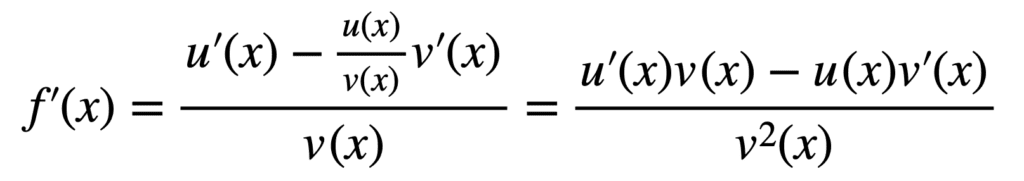
Nous avions vu comment trouver la dérivée des fonctions sinus et cosinus. En utilisant la règle du quotient, nous pouvons maintenant trouver également la dérivée de la fonction tangente :

F(X) = bronzé X = péché X / cos X

En appliquant la règle du quotient et en simplifiant l’expression résultante :

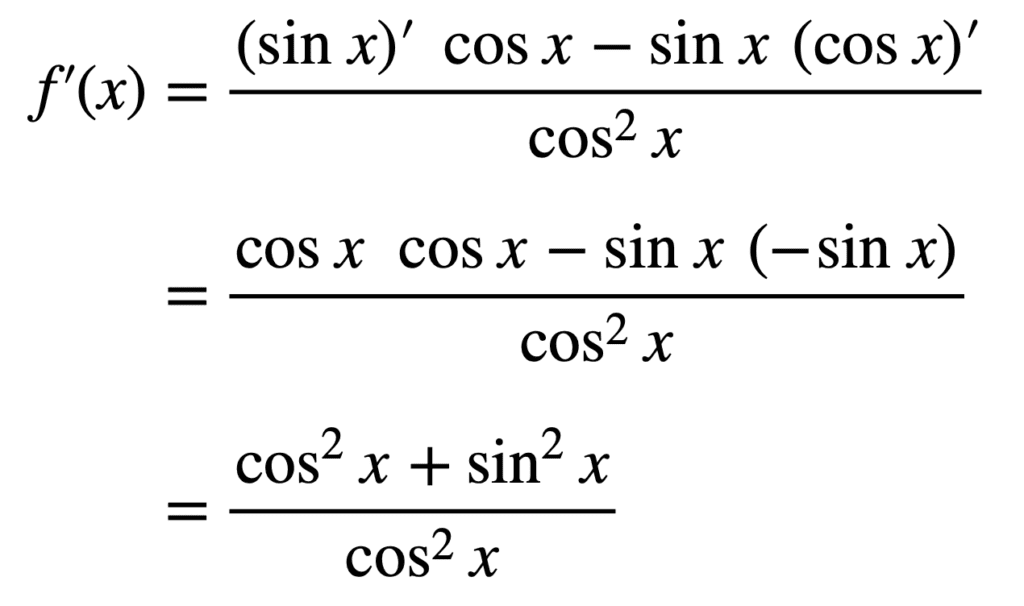
De l’identité pythagoricienne en trigonométrie, nous savons que cos²X + péché²X = 1, d’où :

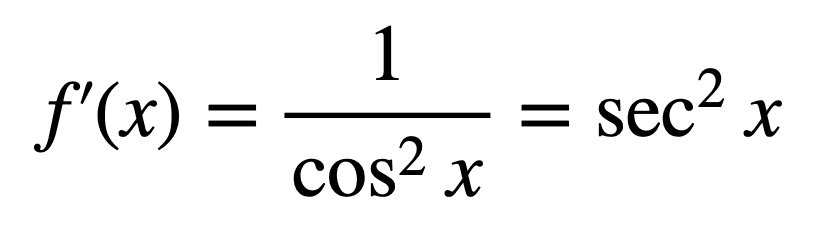
Par conséquent, en utilisant la règle du quotient, nous avons facilement trouvé que la dérivée de la tangente est la fonction sécante au carré.

Lectures complémentaires

Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.

Livres

Des articles

Résumé

Dans ce tutoriel, vous avez découvert comment appliquer les règles de puissance, de produit et de quotient pour trouver la dérivée des fonctions.

Concrètement, vous avez appris :

• La règle de puissance à suivre pour trouver la dérivée d’une base variable, élevée à une puissance fixe.
• Comment la règle du produit nous permet de trouver la dérivée d’une fonction définie comme le produit de deux autres fonctions (ou plus).
• Comment la règle du quotient nous permet de trouver la dérivée d’une fonction qui est le rapport de deux fonctions dérivables.

Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.