[ad_1]
La règle de la chaîne nous permet de trouver la dérivée des fonctions composites.
Il est largement calculé par l’algorithme de rétropropagation, afin d’entraîner les réseaux de neurones à action directe. En appliquant la règle de la chaîne de manière efficace tout en suivant un ordre d’opérations précis, l’algorithme de rétropropagation calcule le gradient d’erreur de la fonction de perte par rapport à chaque poids du réseau.
Dans ce tutoriel, vous découvrirez la règle de calcul en chaîne pour les fonctions univariées et multivariées.
Après avoir terminé ce tutoriel, vous saurez :
- Une fonction composite est la combinaison de deux (ou plus) fonctions.
- La règle de la chaîne nous permet de trouver la dérivée d’une fonction composite.
- La règle de la chaîne peut être généralisée aux fonctions multivariées, et représentée par un diagramme en arbre.
- La règle de la chaîne est largement appliquée par l’algorithme de rétropropagation afin de calculer le gradient d’erreur de la fonction de perte par rapport à chaque poids.
Commençons.

La règle de la chaîne de calcul pour les fonctions univariées et multivariées
Photo de Pascal Debrunner, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en quatre parties ; ils sont:
- Fonctions composites
- La règle de la chaîne
- La règle de la chaîne généralisée
- Application en apprentissage automatique
Conditions préalables
Pour ce tutoriel, nous supposons que vous savez déjà ce que sont :
Vous pouvez revoir ces concepts en cliquant sur les liens ci-dessus.
Fonctions composites
Nous avons, jusqu’à présent, rencontré des fonctions de variables simples et multiples (appelées, univarié et multivarié fonctions, respectivement). Nous allons maintenant étendre à la fois leur composite formes. Nous verrons, éventuellement, comment appliquer la règle de la chaîne afin de trouver leur dérivée, mais plus à ce sujet sous peu.
Une fonction composite est la combinaison de deux fonctions.
– Page 49, Calcul pour les nuls, 2016.
Considérons deux fonctions d’une seule variable indépendante, F(X) = 2X – 1 et g(X) = X3. Leur fonction composite peut être définie comme suit :
h = g(F(X))
Dans cette opération, g est fonction de F. Cela signifie que g est appliqué au résultat de l’application de la fonction, F, à X, produisant h.
Considérons un exemple concret utilisant les fonctions spécifiées ci-dessus pour mieux comprendre cela.
Supposer que F(X) et g(X) sont deux systèmes en cascade, recevant une entrée X = 5 :

Deux systèmes en cascade représentant une fonction composite
Depuis F(X) est le premier système de la cascade (car c’est la fonction interne du composite), sa sortie est calculée en premier :
F(5) = (2 × 5) – 1 = 9
Ce résultat est ensuite transmis en entrée à g(X), le deuxième système de la cascade (car c’est la fonction externe dans le composite) pour produire le résultat net de la fonction composite :
g(9) = 93 = 729
Nous aurions pu, alternativement, calculer le résultat net en une seule fois, si nous avions effectué le calcul suivant :
h = g(F(X)) = (2X – 1)3 = 729
La composition des fonctions peut également être considérée comme un enchaînement processus, pour utiliser un terme plus familier, où la sortie d’une fonction alimente la suivante dans la chaîne.
Avec les fonctions composites, l’ordre compte.
– Page 49, Calcul pour les nuls, 2016.
Gardez à l’esprit que la composition des fonctions est un non commutatif processus, ce qui signifie que l’échange de l’ordre de F(X) et g(X) dans la cascade (ou la chaîne) ne produit pas les mêmes résultats. D’où:
g(F(X)) F(g(X))
La composition des fonctions peut également être étendue au cas multivarié :
h = g(r, s, t) = g(r(x, y), s(x, y), t(x, y)) = g(F(x, y))
Ici, F(x, y) est une fonction vectorielle de deux variables indépendantes (ou entrées), X et oui. Il est composé de trois composants (pour cet exemple particulier) qui sont r(x, y), s(x, y) et t(x, y), et qui sont également connus sous le nom de composant fonctions de F.
Cela signifie que F(X, oui) mappera deux entrées sur trois sorties, puis alimentera ces trois sorties dans le système consécutif de la chaîne, g(r, s, t), produire h.
La règle de la chaîne
La règle de la chaîne nous permet de trouver la dérivée d’une fonction composite.
Définissons d’abord comment la règle de chaîne différencie une fonction composite, puis divisons-la en ses composants séparés pour mieux la comprendre. Si nous devions reconsidérer la fonction composée, h = g(F(X)), alors sa dérivée telle que donnée par la règle de la chaîne est :

Ici, vous est la sortie de la fonction interne F (Par conséquent, vous = F(X)), qui est ensuite transmis en entrée à la fonction suivante g produire h (Par conséquent, h = g(vous)). Remarquez donc comment la règle de la chaîne relie la production nette, h, à l’entrée, X, à travers un variable intermédiaire, vous.
Rappelons que la fonction composite est définie comme suit :
h(X) = g(F(X)) = (2X – 1)3
Le premier élément de la règle de la chaîne, dh / du, nous dit de commencer par trouver la dérivée de la partie externe de la fonction composite, tout en ignorant tout ce qui se trouve à l’intérieur. Pour cela, on appliquera la règle de puissance :
((2X – 1)3)’ = 3(2X – 1)2
Le résultat est ensuite multiplié par le deuxième composant de la règle de chaîne, du / dx, qui est la dérivée de la partie interne de la fonction composite, cette fois en ignorant tout ce qui est à l’extérieur :
( (2X – 1)’ )3 = 2
La dérivée de la fonction composite telle que définie par la règle de la chaîne est alors la suivante :
h‘ = 3(2X – 1)2 × 2 = 6(2X – 1)2
Nous avons, ici, considéré un exemple simple, mais le concept d’application de la règle de chaîne à des fonctions plus compliquées reste le même. Nous examinerons des fonctions plus difficiles dans un didacticiel séparé.
La règle de la chaîne généralisée
On peut généraliser la règle de la chaîne au-delà du cas univarié.
Considérons le cas où X ℝm et vous ℝm, ce qui signifie que la fonction interne, F, Plans m entrées à m sorties, tandis que la fonction externe, g, reçoit m entrées pour produire une sortie, h. Pour je = 1, …, m la règle de la chaîne généralisée stipule :

Ou sous sa forme plus compacte, par j = 1, …, m:
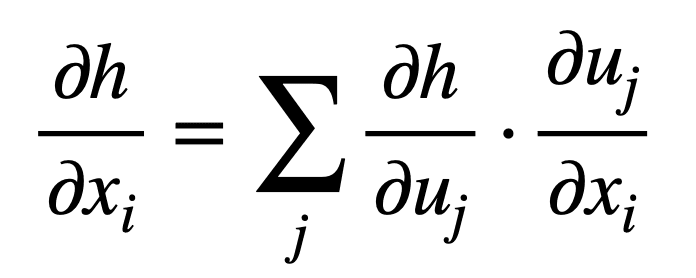
Rappelons que nous employons l’utilisation de dérivées partielles lorsque nous trouvons le gradient d’une fonction de plusieurs variables.
On peut également visualiser le fonctionnement de la règle de chaîne par un diagramme en arbre.
Supposons que nous ayons une fonction composée de deux variables indépendantes, X1 et X2, défini comme suit :
h = g(F(X1, X2)) = g(vous1(X1, X2), vous2(X1, X2))
Ici, vous1 et vous2 jouent le rôle de variables intermédiaires. Son arborescence serait représentée comme suit :
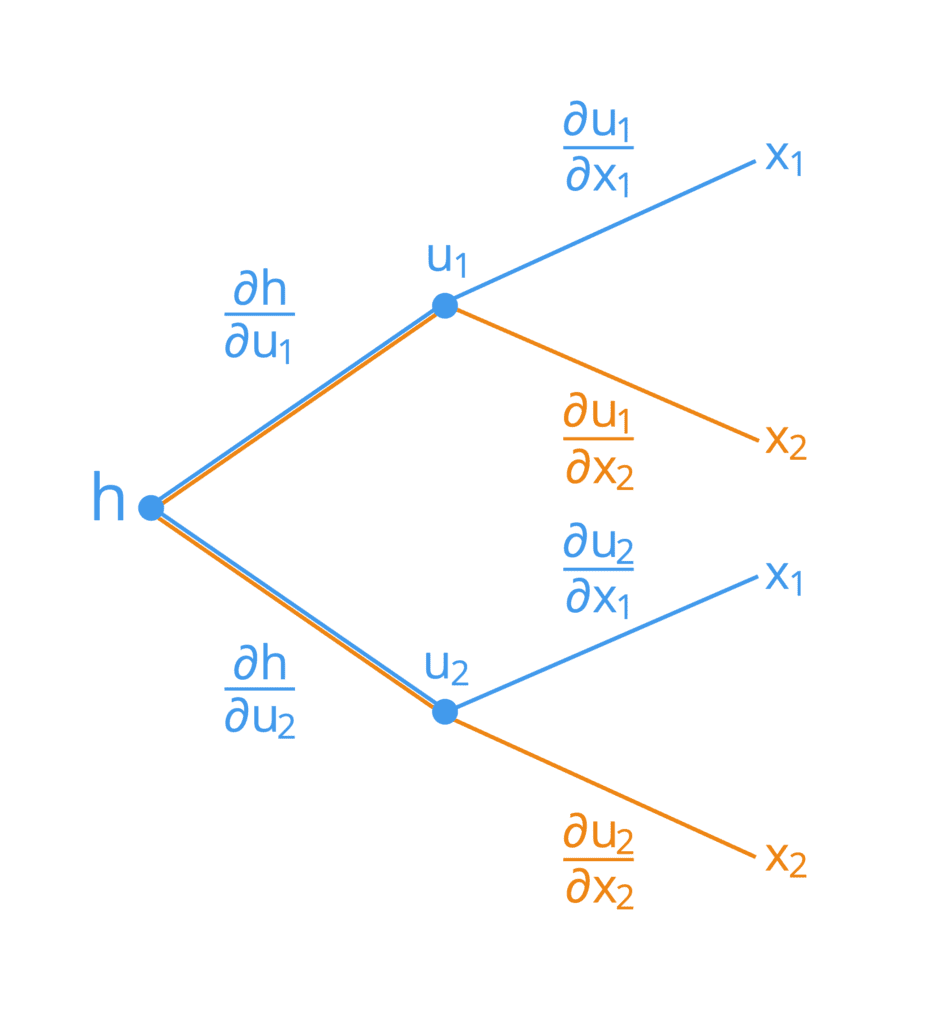
Représentation de la règle de chaîne par un diagramme en arbre
Afin de dériver la formule pour chacune des entrées, X1 et X2, nous pouvons partir du côté gauche de l’arborescence et suivre ses branches vers la droite. De cette manière, nous constatons que nous formons les deux formules suivantes (les branches étant résumées ont été codées par couleur pour plus de simplicité):

Remarquez comment la règle de la chaîne relie la sortie nette, h, à chacune des entrées, Xje, à travers les variables intermédiaires, vousj. C’est un concept que l’algorithme de rétropropagation applique largement pour optimiser les poids d’un réseau de neurones.
Application en apprentissage automatique
Observez à quel point le diagramme en arbre est similaire à la représentation typique d’un réseau de neurones (bien que nous représentions généralement ce dernier en plaçant les entrées sur le côté gauche et les sorties sur le côté droit). Nous pouvons appliquer la règle de la chaîne à un réseau de neurones grâce à l’utilisation de l’algorithme de rétropropagation, d’une manière très similaire à la façon dont nous l’avons appliquée au diagramme en arbre ci-dessus.
Un domaine où la règle de la chaîne est utilisée à l’extrême est l’apprentissage en profondeur, où la valeur de la fonction oui est calculé comme une composition de fonctions à plusieurs niveaux.
– Page 159, Mathématiques pour l’apprentissage automatique, 2020.
Un réseau de neurones peut, en effet, être représenté par une fonction composite emboîtée massive. Par exemple:
oui = FK ( FK-1 ( … ( F1(X)) … ))
Ici, X sont les entrées du réseau de neurones (par exemple, les images) alors que oui sont les sorties (par exemple, les étiquettes de classe). Chaque fonction, Fje, pour je = 1, …, K, se caractérise par ses propres poids.
L’application de la règle de la chaîne à une telle fonction composite nous permet de travailler en arrière à travers toutes les couches cachées constituant le réseau de neurones et de calculer efficacement le gradient d’erreur de la fonction de perte par rapport à chaque poids, wje, du réseau jusqu’à ce que nous arrivions à l’entrée.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Livres
Résumé
Dans ce didacticiel, vous avez découvert la règle de calcul en chaîne pour les fonctions univariées et multivariées.
Concrètement, vous avez appris :
- Une fonction composite est la combinaison de deux (ou plus) fonctions.
- La règle de la chaîne nous permet de trouver la dérivée d’une fonction composite.
- La règle de la chaîne peut être généralisée aux fonctions multivariées, et représentée par un diagramme en arbre.
- La règle de la chaîne est largement appliquée par l’algorithme de rétropropagation afin de calculer le gradient d’erreur de la fonction de perte par rapport à chaque poids.
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.