[ad_1]
Les fonctions à valeur vectorielle sont souvent rencontrées dans l’apprentissage automatique, l’infographie et les algorithmes de vision par ordinateur. Ils sont particulièrement utiles pour définir les paramétrique équations de courbes spatiales. Il est important d’acquérir une compréhension de base des fonctions vectorielles pour saisir des concepts plus complexes.
Dans ce tutoriel, vous découvrirez ce que sont les fonctions à valeur vectorielle, comment les définir et quelques exemples.
Après avoir terminé ce tutoriel, vous saurez :
- Définition des fonctions à valeur vectorielle
- Dérivées de fonctions vectorielles
Commençons.
Une iIntroduction douce aux fonctions à valeur vectorielle. Photo de Noreen Saeed, certains droits réservés
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; ils sont:
- Définition et exemples de fonctions à valeurs vectorielles
- Différencier les fonctions à valeur vectorielle
Définition d’une fonction à valeur vectorielle
Une fonction à valeur vectorielle est également appelée fonction vectorielle. C’est une fonction avec les deux propriétés suivantes :
- Le domaine est un ensemble de nombres réels
- La plage est un ensemble de vecteurs
Les fonctions vectorielles sont donc simplement une extension des fonctions scalaires, où à la fois le domaine et la plage sont l’ensemble des nombres réels.
Dans ce tutoriel, nous considérerons les fonctions vectorielles dont la plage est l’ensemble des vecteurs à deux ou trois dimensions. Par conséquent, de telles fonctions peuvent être utilisées pour définir un ensemble de points dans l’espace.
Étant donné les vecteurs unitaires i,j,k parallèles aux axes x,y,z respectivement, nous pouvons écrire une fonction vectorielle tridimensionnelle sous la forme :
r
Il peut aussi s’écrire :
r
Les deux notations ci-dessus sont équivalentes et souvent utilisées dans divers manuels.
Courbes spatiales et équations paramétriques
Nous avons défini une fonction vectorielle r
Exemples de fonctions vectorielles
Cette section présente quelques exemples de fonctions vectorielles qui définissent des courbes spatiales. Tous les exemples sont également tracés dans la figure présentée après les exemples.
1.1 Un cercle
Commençons par un exemple simple de fonction vectorielle dans l’espace 2D :
r_1
Ici, les équations paramétriques sont :
x
y
La courbe d’espace définie par le paramétrique équations est un cercle dans l’espace 2D comme le montre la figure. Si nous faisons varier t de -𝜋 à 𝜋, nous générerons tous les points qui se trouvent sur le cercle.
1.2 Une hélice
Nous pouvons étendre la fonction r_1
r_2
1.3 Un cube torsadé
On peut aussi définir une courbe appelée cubique torsadée avec une forme intéressante comme :
r_3
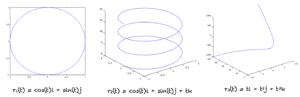
Courbes paramétriques
Dérivées de fonctions vectorielles
Nous pouvons facilement étendre l’idée de la dérivée d’une fonction scalaire à la dérivée d’une fonction vectorielle. Comme l’étendue d’une fonction vectorielle est un ensemble de vecteurs, sa dérivée est aussi un vecteur.
Si
r
alors la dérivée de r
r’
Exemples de dérivées de fonctions vectorielles
On peut trouver les dérivées des fonctions définies dans l’exemple précédent comme :
2.1 Un cercle
L’équation paramétrique d’un cercle en 2D est donnée par :
r_1
Sa dérivée est donc calculée en calculant les dérivées correspondantes de x
x’
y’
Cela nous donne :
r_1′
r_1′
La courbe spatiale définie par les équations paramétriques est un cercle dans l’espace 2D comme le montre la figure. Si nous faisons varier t de -𝜋 à π, nous générerons tous les points qui se trouvent sur le cercle.
2.2 Une hélice
Semblable à l’exemple précédent, nous pouvons calculer la dérivée de r_2
r_2
r_2′
2.3 Un cube torsadé
La dérivée de r_3
r_3
r_3′
Tous les exemples ci-dessus sont montrés dans la figure, où les dérivées sont tracées en rouge. Notez que la dérivée du cercle définit également un cercle dans l’espace.
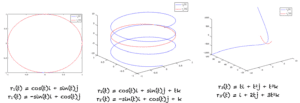
Fonctions paramétriques et leurs dérivées
Exemples plus complexes
Une fois que vous aurez acquis une compréhension de base de ces fonctions, vous pourrez vous amuser à définir diverses formes et courbes dans l’espace. D’autres exemples populaires utilisés par la communauté mathématique sont définis ci-dessous et illustrés dans la figure.
La spire toroïdalemoi :
r_4
Le nœud de trèfle:
r_5
La cardioïde :
r_6
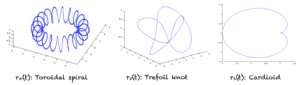
Courbes plus complexes
Importance des fonctions à valeur vectorielle dans l’apprentissage automatique
Les fonctions à valeur vectorielle jouent un rôle important dans les algorithmes d’apprentissage automatique. Étant une extension des fonctions à valeur scalaire, vous les rencontreriez dans des tâches telles que la classification multi-classes et les problèmes multi-étiquettes. Les méthodes du noyau, un domaine important de l’apprentissage automatique, peuvent impliquer le calcul de fonctions à valeur vectorielle, qui peuvent être utilisées ultérieurement dans l’apprentissage multitâche ou l’apprentissage par transfert.
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Thomas’ Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Résumé
Dans ce tutoriel, vous avez découvert ce que sont les fonctions vectorielles et comment les différencier.
Concrètement, vous avez appris :
- Définition des fonctions vectorielles
- Paramétrique courbes
- Différencier les fonctions vectorielles
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.