[ad_1]
Lorsqu’il s’agit de tâches d’apprentissage automatique telles que la classification ou la régression, les techniques d’approximation jouent un rôle clé dans l’apprentissage à partir des données. De nombreuses méthodes d’apprentissage automatique approchent une fonction ou une correspondance entre les entrées et les sorties via un algorithme d’apprentissage.
Dans ce tutoriel, vous découvrirez ce qu’est l’approximation et son importance dans l’apprentissage automatique et la reconnaissance de formes.
Après avoir terminé ce tutoriel, vous saurez :
- Qu’est-ce que l’approximation
- Importance de l’approximation dans l’apprentissage automatique
Commençons.
Une introduction douce à l’approximation. Photo de M Mani, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en 3 parties ; elles sont:
- Qu’est-ce que l’approximation ?
- Approximation lorsque la forme de la fonction n’est pas connue
- Approximation lorsque la forme de la fonction est connue
Qu’est-ce que l’approximation ?
Nous rencontrons très souvent des approximations. Par exemple, le nombre irrationnel peut être approximé par le nombre 3,14. Une valeur plus précise est 3,141593, ce qui reste une approximation. Vous pouvez de la même manière approximer les valeurs de tous les nombres irrationnels comme sqrt(3), sqrt(7), etc.
L’approximation est utilisée chaque fois qu’une valeur numérique, un modèle, une structure ou une fonction est soit inconnue ou difficile à calculer. Dans cet article, nous allons nous concentrer sur l’approximation des fonctions et décrire son application aux problèmes d’apprentissage automatique. Il y a deux cas différents :
- La fonction est connue mais il est difficile ou numériquement coûteux de calculer sa valeur exacte. Dans ce cas, des méthodes d’approximation sont utilisées pour trouver des valeurs proches des valeurs réelles de la fonction.
- La fonction elle-même est inconnue et, par conséquent, un modèle ou un algorithme d’apprentissage est utilisé pour trouver de près une fonction qui peut produire des sorties proches des sorties de la fonction inconnue.
Approximation lorsque la forme de la fonction est connue
Si la forme d’une fonction est connue, alors une méthode bien connue en calcul et en mathématiques est l’approximation via les séries de Taylor. La série de Taylor d’une fonction est la somme de termes infinis, qui sont calculés en utilisant les dérivées de la fonction. Le développement en série de Taylor d’une fonction est abordé dans ce didacticiel.
Une autre méthode d’approximation bien connue en calcul et en mathématiques est la méthode de Newton. Il peut être utilisé pour approximer les racines de polynômes, ce qui en fait une technique utile pour estimer des quantités telles que la racine carrée de différentes valeurs ou l’inverse de différents nombres, etc.
Approximation lorsque la forme de la fonction est inconnue
En science des données et en apprentissage automatique, on suppose qu’il existe une fonction sous-jacente qui détient la clé de la relation entre les entrées et les sorties. La forme de cette fonction est inconnue. Ici, nous discutons de plusieurs problèmes d’apprentissage automatique qui utilisent l’approximation.
Approximation en régression
La régression implique la prédiction d’une variable de sortie lorsqu’on lui donne un ensemble d’entrées. Dans la régression, la fonction qui mappe véritablement les variables d’entrée aux sorties n’est pas connue. On suppose qu’un modèle de régression linéaire ou non linéaire peut approximer le mappage des entrées aux sorties.
Par exemple, nous pouvons disposer de données relatives aux calories consommées par jour et à la glycémie correspondante. Pour décrire la relation entre l’apport calorique et la production de sucre dans le sang, nous pouvons supposer une relation linéaire/fonction de cartographie. La droite est donc l’approximation du mappage des entrées aux sorties. Une méthode d’apprentissage telle que la méthode des moindres carrés est utilisée pour trouver cette droite.
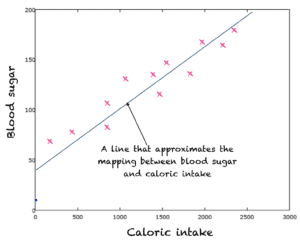
Une approximation en ligne droite de la relation entre le nombre de calories et la glycémie
Approximation dans la classification
Un exemple classique de modèles qui se rapprochent des fonctions dans les problèmes de classification est celui des réseaux de neurones. On suppose que le réseau de neurones dans son ensemble peut approximer une vraie fonction qui mappe les entrées aux étiquettes de classe. La descente de gradient ou un autre algorithme d’apprentissage est ensuite utilisé pour apprendre cette approximation de la fonction en ajustant les poids du réseau neuronal.
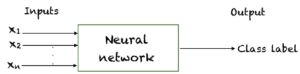
Un réseau de neurones se rapproche d’une fonction sous-jacente qui mappe les entrées aux sorties
Approximation dans l’apprentissage non supervisé
Vous trouverez ci-dessous un exemple typique d’apprentissage non supervisé. Ici, nous avons des points dans l’espace 2D et l’étiquette d’aucun de ces points n’est donnée. Un algorithme de clustering suppose généralement un modèle selon lequel un point peut être affecté à une classe ou une étiquette. Par exemple, k-means apprend les étiquettes des données en supposant que les clusters de données sont circulaires et, par conséquent, attribue la même étiquette ou classe aux points situés dans le même cercle ou une n-sphère en cas de données multidimensionnelles. Dans la figure ci-dessous, nous approchons la relation entre les points et leurs étiquettes via des fonctions circulaires.
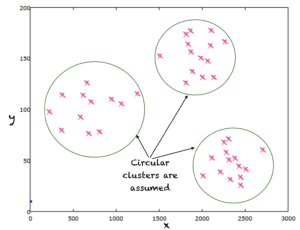
Un algorithme de clustering se rapproche d’un modèle qui détermine des clusters ou des étiquettes inconnues de points d’entrée
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
- Série Maclaurin
- La série de Taylor
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
Sommaire
Dans ce tutoriel, vous avez découvert ce qu’est l’approximation. Concrètement, vous avez appris :
- Approximation
- Approximation lorsque la forme d’une fonction est connue
- Approximation lorsque la forme d’une fonction est inconnue
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre