[ad_1]
Une introduction douce à la série Taylor
L’expansion de la série de Taylor est un concept génial, non seulement dans le monde des mathématiques, mais aussi dans la théorie de l’optimisation, l’approximation des fonctions et l’apprentissage automatique. Il est largement appliqué dans les calculs numériques lorsque des estimations des valeurs d’une fonction à différents points sont nécessaires.
Dans ce tutoriel, vous découvrirez les séries de Taylor et comment approximer les valeurs d’une fonction autour de différents points en utilisant son développement en série de Taylor.
Après avoir terminé ce tutoriel, vous saurez :
- Développement en série de Taylor d’une fonction
- Comment approximer des fonctions en utilisant le développement en série de Taylor
Commençons.
Une introduction douce à la série Taylor. Photo de Muhammad Khubaib Sarfraz, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en 3 parties ; elles sont:
- Série Power et série Taylor
- Polynômes de Taylor
- Approximation de fonction à l’aide de polynômes de Taylor
Qu’est-ce qu’une série de puissance ?
Ce qui suit est une série entière sur le centre x=a et les coefficients constants c_0, c_1, etc.
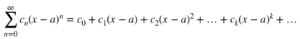
Qu’est-ce qu’une série Taylor ?
C’est un fait étonnant que des fonctions infiniment dérivables puissent générer une série de puissances appelée série de Taylor. Supposons que nous ayons une fonction f(x) et que f(x) ait des dérivées de tous les ordres sur un intervalle donné, alors la série de Taylor générée par f(x) à x=a est donnée par :
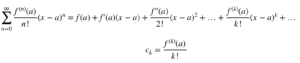
La deuxième ligne de l’expression ci-dessus donne la valeur du kième coefficient.
Si nous posons a=0, alors nous avons un développement appelé développement en série de Maclaurin de f(x).
Exemples d’extension de la série Taylor
Les séries de Taylor générées par f(x) = 1/x peuvent être trouvées en différenciant d’abord la fonction et en trouvant une expression générale pour la dérivée k.
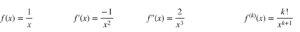
La série Taylor sur divers points peut maintenant être trouvée. Par exemple:
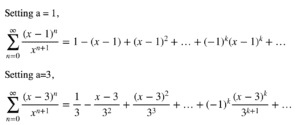
Polynôme de Taylor
Un polynôme de Taylor d’ordre k, engendré par f(x) en x=a est donné par :
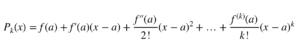
Pour l’exemple de f(x)=1/x, le polynôme de Taylor d’ordre 2 est donné par :
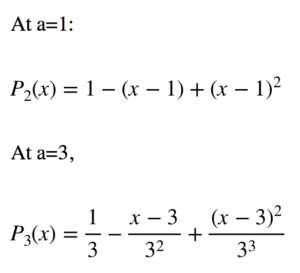
Approximation via les polynômes de Taylor
Nous pouvons approximer la valeur d’une fonction en un point x=a en utilisant des polynômes de Taylor. Plus l’ordre du polynôme est élevé, plus les termes du polynôme sont nombreux et plus l’approximation est proche de la valeur réelle de la fonction à ce point.
Dans le graphique ci-dessous, la fonction 1/x est tracée autour du point x=1 (gauche) et x=3 (droite). La ligne en vert est la fonction réelle f(x)= 1/x. La ligne rose représente l’approximation via un polynôme d’ordre 2.
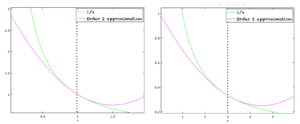
La fonction réelle (vert) et son approximation (rose)
Plus d’exemples de séries Taylor
Regardons la fonction g(x) = e^x. En notant le fait que la dérivée d’ordre k de g(x) est aussi g(x), le développement de g(x) autour de x=a, est donné par :
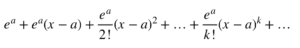
Ainsi, autour de x=0, le développement en série de g(x) est donné par (obtenu en fixant a=0) :
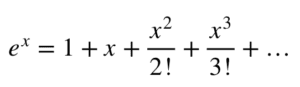
Le polynôme d’ordre k généré pour la fonction e^x autour du point x=0 est donné par :
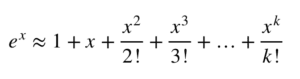
Les graphiques ci-dessous montrent des polynômes de différents ordres qui estiment la valeur de e^x autour de x=0. Nous pouvons voir que lorsque nous nous éloignons de zéro, nous avons besoin de plus de termes pour approximer e^x plus précisément. La ligne verte représentant la fonction réelle se cache derrière la ligne bleue du polynôme approximatif d’ordre 7.
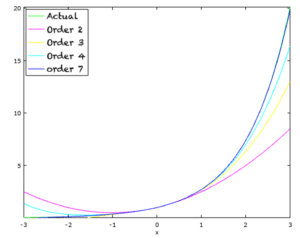
Polynômes de degrés divers qui se rapprochent de e^x
Série Taylor en apprentissage automatique
Une méthode populaire en apprentissage automatique pour trouver les points optimaux d’une fonction est la méthode de Newton. La méthode de Newton utilise les polynômes du second ordre pour approximer la valeur d’une fonction en un point. De telles méthodes qui utilisent des dérivées du second ordre sont appelées algorithmes d’optimisation du second ordre.
Rallonges
Cette section répertorie quelques idées pour étendre le didacticiel que vous souhaiterez peut-être explorer.
- La méthode de Newton
- Algorithmes d’optimisation du second ordre
Si vous explorez l’une de ces extensions, j’aimerais le savoir. Postez vos découvertes dans les commentaires ci-dessous.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Tutoriels
Ressources
Livres
- Reconnaissance de formes et apprentissage automatique par Christopher M. Bishop.
- Apprentissage approfondi par Ian Goodfellow, Joshua Begio, Aaron Courville.
- Thomas Calculus, 14e édition, 2017. (basé sur les travaux originaux de George B. Thomas, révisés par Joel Hass, Christopher Heil, Maurice Weir)
- Calcul, 3e édition, 2017. (Gilbert Strang)
- Calculus, 8e édition, 2015. (James Stewart)
Sommaire
Dans ce didacticiel, vous avez découvert ce qu’est le développement en série de Taylor d’une fonction autour d’un point. Concrètement, vous avez appris :
- Série Power et série Taylor
- Polynômes de Taylor
- Comment approximer des fonctions autour d’une valeur en utilisant des polynômes de Taylor
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre