Dernière mise à jour le 3 décembre 2021

Ce tutoriel est une extension de Method Of Lagrange Multipliers: The Theory Behind Support Vector Machines (Partie 1: The Separable Case)) et explique le cas non séparable. Dans les problèmes de la vie réelle, les exemples d’entraînement positifs et négatifs peuvent ne pas être complètement séparables par une limite de décision linéaire. Ce tutoriel explique comment créer une marge souple qui tolère un certain nombre d’erreurs.

Dans ce didacticiel, nous couvrirons les bases d’une SVM linéaire. Nous n’entrerons pas dans les détails des SVM non linéaires dérivés à l’aide de l’astuce du noyau. Le contenu est suffisant pour comprendre le modèle mathématique de base derrière un classificateur SVM.

Après avoir terminé ce tutoriel, vous saurez :

• Concept d’une marge douce
• Comment maximiser la marge tout en permettant des erreurs de classement
• Comment formuler le problème d’optimisation et calculer le dual de Lagrange

Commençons.

Présentation du didacticiel

Ce tutoriel est divisé en 2 parties ; ils sont:

1. La solution du problème SVM pour le cas où les exemples positifs et négatifs ne sont pas linéairement séparables
   1. L’hyperplan séparateur et les contraintes relâchées correspondantes
   2. Le problème d’optimisation quadratique pour trouver la marge souple
2. Un exemple travaillé

Conditions préalables

Pour ce didacticiel, nous partons du principe que vous êtes déjà familiarisé avec les sujets suivants. Vous pouvez cliquer sur les liens individuels pour obtenir plus d’informations.

Notations utilisées dans ce didacticiel

Il s’agit d’une continuation de la partie 1, donc les mêmes notations seront utilisées.

• $m$ : Total des points de formation
• $x$ : point de données, qui est un vecteur de dimension $n$. Chaque dimension est indexée par j.
• $x^+$ : Exemple positif
• $x^-$ : exemple négatif
• $i$ : Indice utilisé pour indexer les points d’entraînement. $0 leq i < m$
• $j$ : Indice pour indexer une dimension du point de données. $1 leq j leq n$
• $t$ : Libellé des points de données. C’est un vecteur de dimension m
• $T$ : opérateur de transposition
• $w$ : Vecteur de poids désignant les coefficients de l’hyperplan. C’est un vecteur de dimension n$
• $alpha$ : vecteur de multiplicateurs de Lagrange, un vecteur de dimension $m$
• $mu$ : vecteur de multiplicateurs de Lagrange, encore un vecteur de dimension $m$
• $xi$ : erreur de classification. Un vecteur de dimension $m$

L’hyperplan de séparation et l’assouplissement des contraintes

Trouvons un hyperplan de séparation entre les exemples positifs et négatifs. Pour rappel, l’hyperplan séparateur est donné par l’expression suivante, avec (w_j) étant les coefficients et (w_0) étant la constante arbitraire qui détermine la distance de l’hyperplan à l’origine :

$$
w^T x_i + w_0 = 0
$$

Comme nous permettons aux exemples positifs et négatifs de se trouver du mauvais côté de l’hyperplan, nous avons un ensemble de contraintes relâchées. En définissant $xi_i geq 0, forall i$, pour des exemples positifs, nous avons besoin de :

$$
w^T x_i^+ + w_0 geq 1 – xi_i
$$

Aussi pour les exemples négatifs, nous avons besoin de :

$$
w^T x_i^- + w_0 leq -1 + xi_i
$$

En combinant les deux contraintes ci-dessus en utilisant l’étiquette de classe $t_i in {-1,+1}$, nous avons la contrainte suivante pour tous les points :

$$
t_i(w^T x_i + w_0) geq 1 – xi_i
$$

La variable $xi$ permet plus de flexibilité dans notre modèle. Il a les interprétations suivantes :

1. $xi_i =0$ : Cela signifie que $x_i$ est correctement classé et que ce point de données est du bon côté de l’hyperplan et loin de la marge.
2. $0 < xi_i < 1$ : Lorsque cette condition est remplie, $x_i$ se trouve du bon côté de l'hyperplan mais à l'intérieur de la marge.
3. $xi_i > 0$ : La satisfaction de cette condition implique que $x_i$ est mal classé.

Par conséquent, $xi$ quantifie les erreurs dans la classification des points d’entraînement. Nous pouvons définir l’erreur logicielle comme suit :

$$
E_{soft} = sum_i xi_i
$$

Le problème de la programmation quadratique

Nous sommes maintenant en mesure de formuler la fonction objectif avec les contraintes qui s’y rattachent. Nous voulons toujours maximiser la marge, c’est-à-dire minimiser la norme du vecteur de poids. Parallèlement à cela, nous voulons également garder l’erreur logicielle aussi petite que possible. Par conséquent, notre nouvelle fonction objectif est maintenant donnée par l’expression suivante, avec $C$ étant une constante définie par l’utilisateur et représente le facteur de pénalité ou la constante de régularisation.

$$
frac{1}{2}||w||^2 + C sum_i xi_i
$$

Le problème de programmation quadratique global est donc donné par l’expression suivante :

$$
min_w frac{1}{2}||w||^2 + C sum_i xi_i ;text{ soumis à } t_i(w^Tx_i+w_0) geq +1 – xi_i, forall i ; text{ et } xi_i geq 0, forall i
$$

Le rôle de C, la constante de régularisation

Pour comprendre le facteur de pénalité $C$, considérons le terme produit $C sum_i xi_i$, qui doit être minimisé. Si C reste grand, alors la marge souple $sum_i xi_i$ sera automatiquement petite. Si $C$ est proche de zéro, alors nous permettons à la marge souple d’être importante, ce qui rend le produit global petit.

En bref, une grande valeur de $C$ signifie que nous avons une pénalité élevée sur les erreurs et donc notre modèle n’est pas autorisé à faire trop d’erreurs de classification. Une petite valeur de $C$ permet aux erreurs de croître.

Solution via la méthode des multiplicateurs de Lagrange

Utilisons la méthode des multiplicateurs de Lagrange pour résoudre le problème de programmation quadratique que nous avons formulé précédemment. La fonction de Lagrange est donnée par :

$$
L(w, w_0, alpha, mu) = frac{1}{2}||w||^2 + sum_i alpha_ibig(t_i(w^Tx_i+w_0) – 1 + xi_i grand) – sum_i mu_i xi_i
$$

Pour résoudre ce qui précède, nous définissons les éléments suivants :
begin{équation}
frac{partial L}{ partial w} = 0, \
frac{partial L}{ partial alpha} = 0, \
frac{partial L}{ partial w_0} = 0, \
frac{partial L}{ partial mu} = 0 \
end{équation}

La résolution de ce qui précède nous donne :
$$
w = sum_i alpha_i t_i x_i
$$
et
$$
0= C – alpha_i – mu_i
$$

Substituer ce qui précède dans la fonction de Lagrange nous donne le problème d’optimisation suivant, également appelé le dual :

$$
L_d = -frac{1}{2} sum_i sum_k alpha_i alpha_k t_i t_k (x_i)^T (x_k) + sum_i alpha_i
$$

Nous devons maximiser ce qui précède sous réserve des contraintes suivantes :

begin{équation}
sum_i alpha_i t_i = 0 \ text{ et }
0 leq alpha_i leq C, forall i
end{équation}

Semblable au cas séparable, nous avons une expression pour $w$ en termes de multiplicateurs de Lagrange. La fonction objectif n’implique aucun terme $w$. Il y a un multiplicateur de Lagrange $alpha$ et $mu$ associé à chaque point de données.

Interprétation du modèle mathématique et calcul de $w_0$

Les cas suivants sont vrais pour chaque point de données d’entraînement $x_i$ :

• $alpha_i = 0$ : Le ième point d’entraînement se trouve du bon côté de l’hyperplan loin de la marge. Ce point ne joue aucun rôle dans la classification d’un point test.
• $0 < alpha_i < C$ : Le ième point d'apprentissage est un vecteur de support et se trouve sur la marge. Pour ce point $xi_i = 0$ et $t_i(w^T x_i + w_0) = 1$ et donc il peut être utilisé pour calculer $w_0$. En pratique, $w_0$ est calculé à partir de tous les vecteurs de support et une moyenne est prise.
• $alpha_i = C$ : Le ième point d’apprentissage est soit à l’intérieur de la marge du bon côté de l’hyperplan, soit ce point est du mauvais côté de l’hyperplan.

L’image ci-dessous vous aidera à comprendre les concepts ci-dessus :

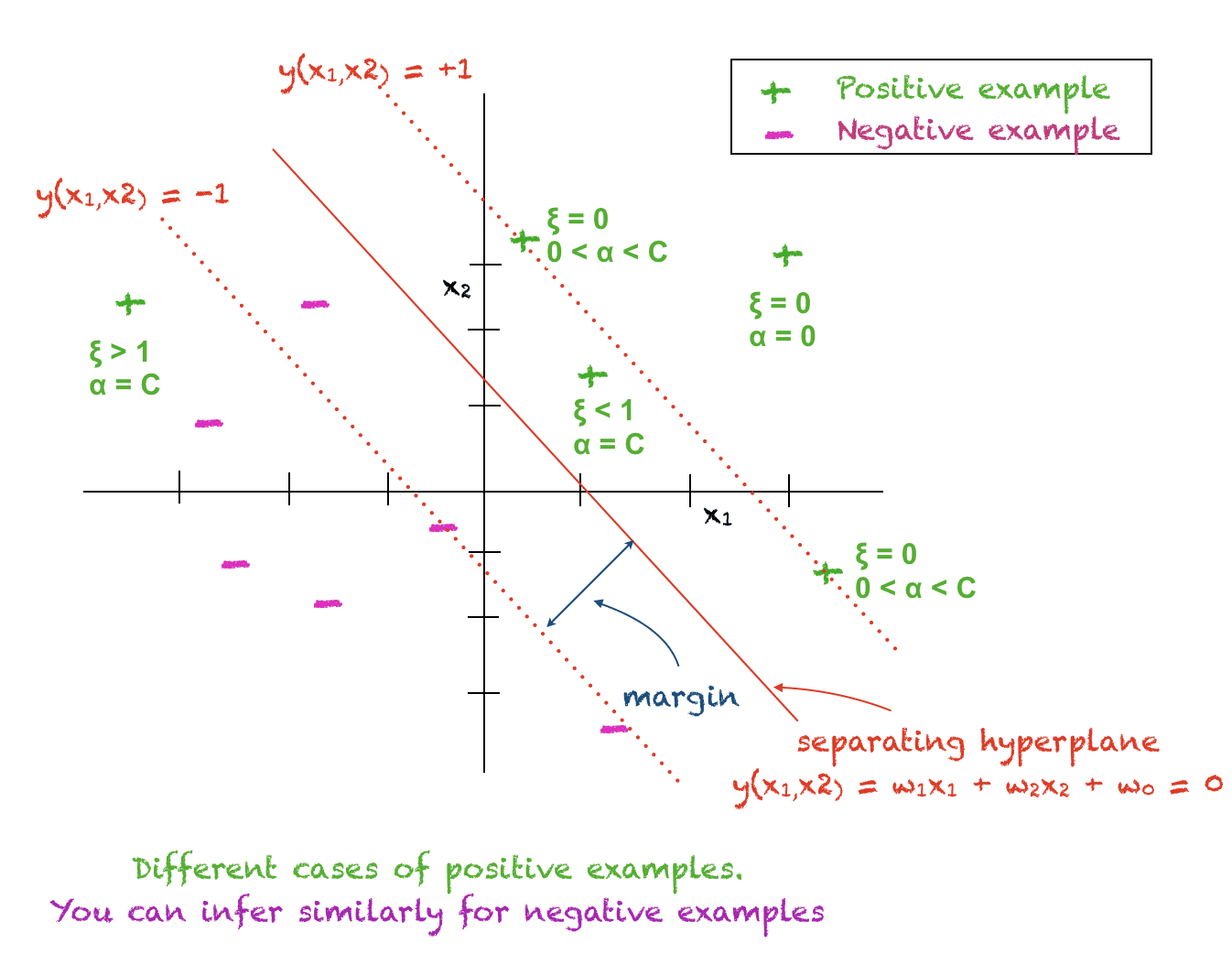
Décider de la classification d’un point de test

La classification de tout point de test $x$ peut être déterminée à l’aide de cette expression :

$$
y(x) = sum_i alpha_i t_i x^T x_i + w_0
$$

Une valeur positive de $y(x)$ implique $xin+1$ et une valeur négative signifie $xin-1$. Par conséquent, la classe prédite d’un point de test est le signe de $y(x)$.

Conditions de Karush-Kuhn-Tucker

Les conditions de Karush-Kuhn-Tucker (KKT) sont satisfaites par le problème d’optimisation sous contraintes ci-dessus tel que donné par :
begin{eqnarray}
alpha_i &geq& 0 \
t_i y(x_i) -1 + xi_i &geq& 0 \
alpha_i(t_i y(x_i) -1 + xi_i) &=& 0 \
mu_i geq 0 \
xi_i geq 0 \
mu_ixi_i = 0
end{eqnarray}

Un exemple résolu

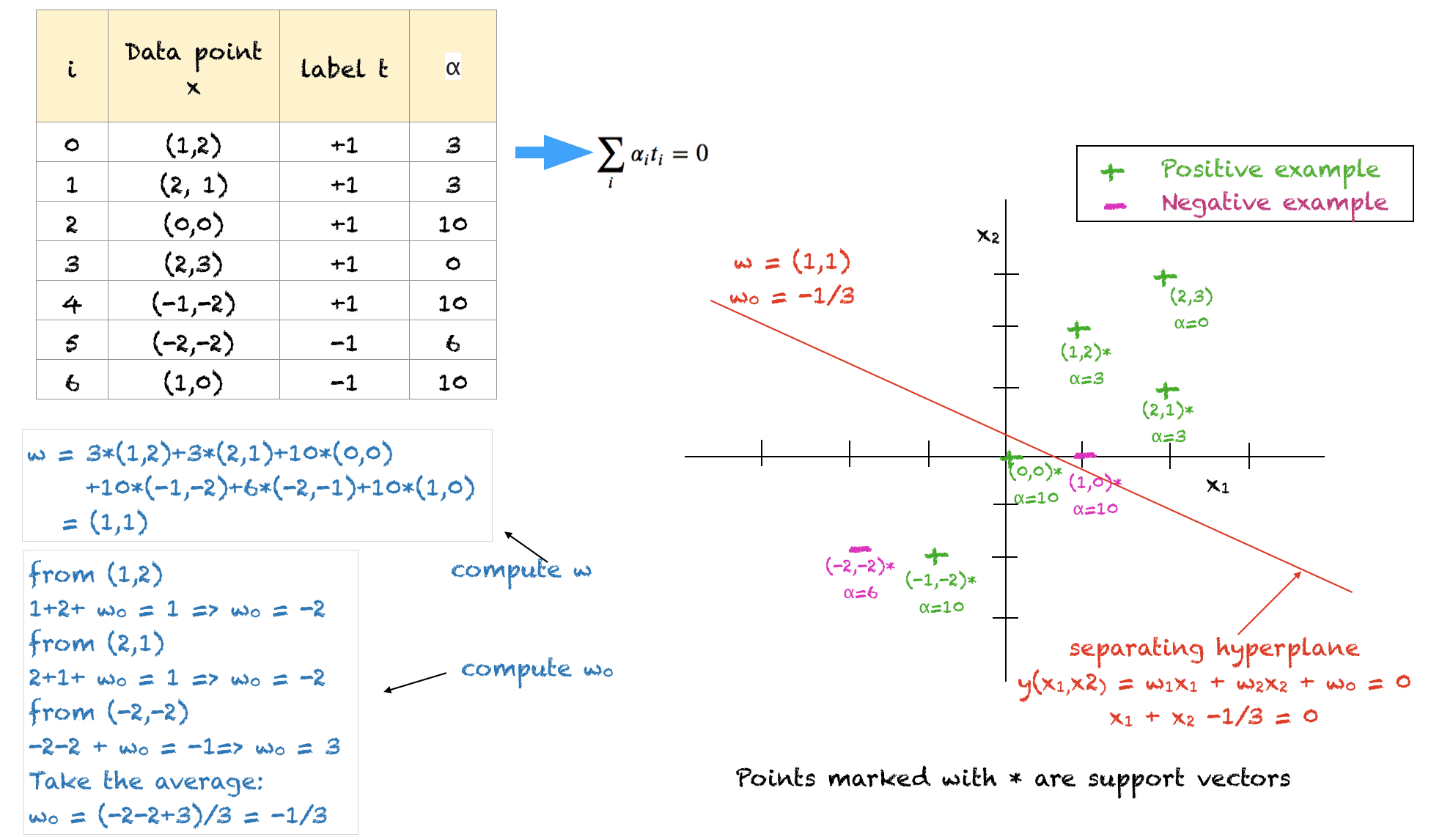
Ci-dessus, un exemple résolu de points d’entraînement 2D pour illustrer tous les concepts. Quelques points à noter à propos de cette solution sont :

• Les points de données d’entraînement et leurs étiquettes correspondantes servent d’entrée
• La constante définie par l’utilisateur $C$ est définie sur 10
• La solution satisfait toutes les contraintes, cependant, ce n’est pas la solution optimale
• Nous devons nous assurer que tous les $alpha$ se situent entre 0 et C
• La somme des alphas de tous les exemples négatifs doit être égale à la somme des alphas de tous les exemples positifs
• Les points (1,2), (2,1) et (-2,-2) se trouvent sur la marge douce du bon côté de l’hyperplan. Leurs valeurs ont été arbitrairement fixées à 3, 3 et 6 respectivement pour équilibrer le problème et satisfaire les contraintes.
• Les points avec $alpha=C=10$ se trouvent soit à l’intérieur de la marge, soit du mauvais côté de l’hyperplan

Lectures complémentaires

Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.

Livres

Des articles

Résumé

Dans ce tutoriel, vous avez découvert la méthode des multiplicateurs de Lagrange pour trouver la marge souple dans un classificateur SVM.

Concrètement, vous avez appris :

• Comment formuler le problème d’optimisation pour le cas non séparable
• Comment trouver l’hyperplan et la marge souple en utilisant la méthode des multiplicateurs de Lagrange
• Comment trouver l’équation de l’hyperplan séparateur pour des problèmes très simples

Avez-vous des questions sur les SVM abordées dans cet article ? Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.