Dernière mise à jour le 26 novembre 2021

Ce didacticiel est conçu pour tous ceux qui souhaitent mieux comprendre comment les multiplicateurs de Lagrange sont utilisés dans la construction du modèle pour les machines à vecteurs de support (SVM). Les SVM ont été initialement conçues pour résoudre des problèmes de classification binaire, puis étendues et appliquées à la régression et à l’apprentissage non supervisé. Ils ont montré leur succès dans la résolution de nombreux problèmes complexes de classification d’apprentissage automatique.

Dans ce didacticiel, nous examinerons le SVM le plus simple qui suppose que les exemples positifs et négatifs peuvent être complètement séparés via un hyperplan linéaire.

Après avoir terminé ce tutoriel, vous saurez :

• Comment l’hyperplan agit comme frontière de décision
• Contraintes mathématiques sur les exemples positifs et négatifs
• Quelle est la marge et comment maximiser la marge
• Rôle des multiplicateurs de Lagrange dans la maximisation de la marge
• Comment déterminer l’hyperplan séparateur pour le cas séparable

Commençons.

Ce tutoriel est divisé en trois parties ; elles sont:

1. Formulation du modèle mathématique de SVM
2. Solution de recherche de l’hyperplan de marge maximale via la méthode des multiplicateurs de Lagrange
3. Exemple résolu pour démontrer tous les concepts

Notations utilisées dans ce didacticiel

• $x$ : point de données, qui est un vecteur à n dimensions.
• $x^+$ : point de données étiqueté +1.
• $x^-$ : point de données étiqueté -1.
• $i$ : Indice utilisé pour indexer les points d’entraînement.
• $t$ : Libellé d’un point de données.
• T : Opérateur de transposition.
• $w$ : Vecteur de poids désignant les coefficients de l’hyperplan. C’est aussi un vecteur à n dimensions.
• $alpha$ : multiplicateurs de Lagrange, un pour chaque point d’entraînement. C’est aussi un vecteur à n dimensions.
• $d$ : Distance perpendiculaire d’un point de données à la limite de décision.

L’hyperplan comme limite de décision

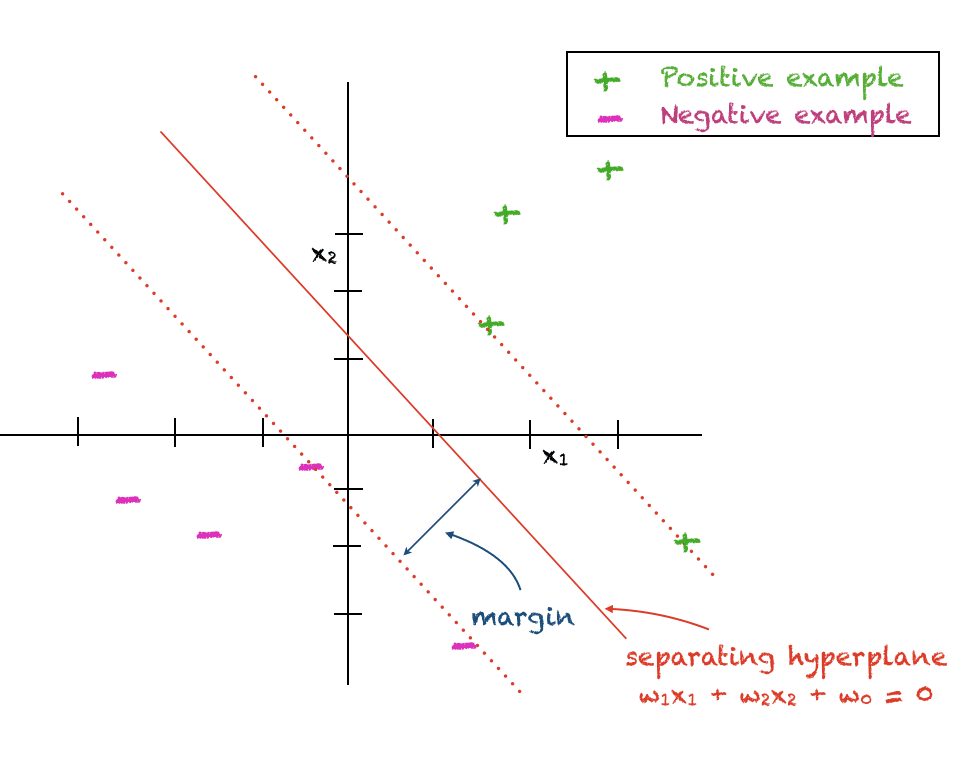
La machine à vecteurs de support est conçue pour discriminer des points de données appartenant à deux classes différentes. Un ensemble de points est étiqueté +1, également appelé classe positive. L’autre ensemble de points est étiqueté -1, également appelé classe négative. Pour l’instant, nous allons faire une hypothèse simplificatrice selon laquelle les points des deux classes peuvent être discriminés via un hyperplan linéaire.

Le SVM suppose une frontière de décision linéaire entre les deux classes et le but est de trouver un hyperplan qui donne la séparation maximale entre les deux classes. Pour cette raison, le terme alternatif maximum margin classifier est aussi parfois utilisé pour désigner un SVM. La distance perpendiculaire entre le point de données le plus proche et la limite de décision est appelée la margin. Comme la marge sépare complètement les exemples positifs et négatifs et ne tolère aucune erreur, elle est aussi appelée la hard margin.

L’expression mathématique d’un hyperplan est donnée ci-dessous avec (w_i) étant les coefficients et (w_0) étant la constante arbitraire qui détermine la distance de l’hyperplan à l’origine :

$$
w^T x_i + w_0 = 0
$$

Pour le ième point à 2 dimensions $(x_{i1}, x_{i2})$ l’expression ci-dessus se réduit à :
$$
w_1x_{i1} + w_2 x_{i2} + w_0 = 0
$$

Contraintes mathématiques sur les points de données positifs et négatifs

Comme nous cherchons à maximiser la marge entre les points de données positifs et négatifs, nous aimerions que les points de données positifs satisfassent à la contrainte suivante :

$$
w^T x_i^+ + w_0 geq +1
$$

De même, les points de données négatifs doivent satisfaire :

$$
w^T x_i^- + w_0 leq -1
$$

Nous pouvons utiliser une astuce pour écrire une équation uniforme pour les deux ensembles de points en utilisant $t_i in {-1,+1}$ pour désigner l’étiquette de classe du point de données $x_i$ :

$$
t_i(w^T x_i + w_0) geq +1
$$

L’hyperplan de la marge maximale

La distance perpendiculaire $d_i$ d’un point de données $x_i$ à la marge est donnée par :

$$
d_i = frac{|w^T x_i + w_0|}{||w||}
$$

Pour maximiser cette distance, nous pouvons minimiser le carré du dénominateur pour nous donner un problème de programmation quadratique donné par :

$$
min frac{1}{2}||w||^2 ;text{ soumis à } t_i(w^Tx_i+w_0) geq +1, forall i
$$

Solution via la méthode des multiplicateurs de Lagrange

Pour résoudre le problème de programmation quadratique ci-dessus avec des contraintes d’inégalité, nous pouvons utiliser la méthode des multiplicateurs de Lagrange. La fonction de Lagrange est donc :

$$
L(w, w_0, alpha) = frac{1}{2}||w||^2 + sum_i alpha_ibig(t_i(w^Tx_i+w_0) – 1big)
$$

Pour résoudre ce qui précède, nous définissons les éléments suivants :

begin{équation}
frac{partial L}{ partial w} = 0, \
frac{partial L}{ partial alpha} = 0, \
frac{partial L}{ partial w_0} = 0 \
end{équation}

Le branchement ci-dessus dans la fonction Lagrange nous donne le problème d’optimisation suivant, également appelé le dual :

$$
L_d = -frac{1}{2} sum_i sum_k alpha_i alpha_k t_i t_k (x_i)^T (x_k) + sum_i alpha_i
$$

Nous devons maximiser ce qui précède sous réserve des éléments suivants :

$$
w = sum_i alpha_i t_i x_i
$$
et
$$
0=sum_i alpha_i t_i
$$

La bonne chose à propos de ce qui précède est que nous avons une expression pour (w) en termes de multiplicateurs de Lagrange. La fonction objectif n’implique aucun terme $w$. Un multiplicateur de Lagrange est associé à chaque point de données. Le calcul de $w_0$ est également expliqué plus loin.

Décider de la classification d’un point de test

La classification de tout point de test $x$ peut être déterminée à l’aide de cette expression :

$$
y(x) = sum_i alpha_i t_i x^T x_i + w_0
$$

Une valeur positive de $y(x)$ implique $xin+1$ et une valeur négative signifie $xin-1$

Conditions de Karush-Kuhn-Tucker

De plus, les conditions de Karush-Kuhn-Tucker (KKT) sont satisfaites par le problème d’optimisation sous contraintes ci-dessus tel que donné par :
begin{eqnarray}
alpha_i &geq& 0 \
t_i y(x_i) -1 &geq& 0 \
alpha_i(t_i y(x_i) -1) &=& 0
end{eqnarray}

Interprétation des conditions KKT

Les conditions KKT dictent que pour chaque point de données, l’une des conditions suivantes est vraie :

• Le multiplicateur de Lagrange est nul, c’est-à-dire (alpha_i=0). Ce point ne joue donc aucun rôle dans la classification

OU

• $ t_i y(x_i) = 1$ et $alpha_i > 0$ : Dans ce cas, le point de données a un rôle à jouer pour décider de la valeur de $w$. Un tel point est appelé vecteur support.

Calcul w_0

Pour $w_0$, nous pouvons sélectionner n’importe quel vecteur de support $x_s$ et résoudre

$$
t_s y(x_s) = 1
$$

Nous donnant:
$$
t_s(sum_i alpha_i t_i x_s^T x_i + w_0) = 1
$$

Un exemple résolu

Pour vous aider à comprendre les concepts ci-dessus, voici un exemple simple résolu arbitrairement. Bien sûr, pour un grand nombre de points, vous utiliseriez un logiciel d’optimisation pour résoudre ce problème. Aussi, c’est une solution possible qui satisfait toutes les contraintes. La fonction objectif peut être maximisée davantage mais la pente de l’hyperplan restera la même pour une solution optimale. De plus, pour cet exemple, $w_0$ a été calculé en prenant la moyenne de $w_0$ des trois vecteurs de support.

Cet exemple vous montrera que le modèle n’est pas aussi complexe qu’il y paraît.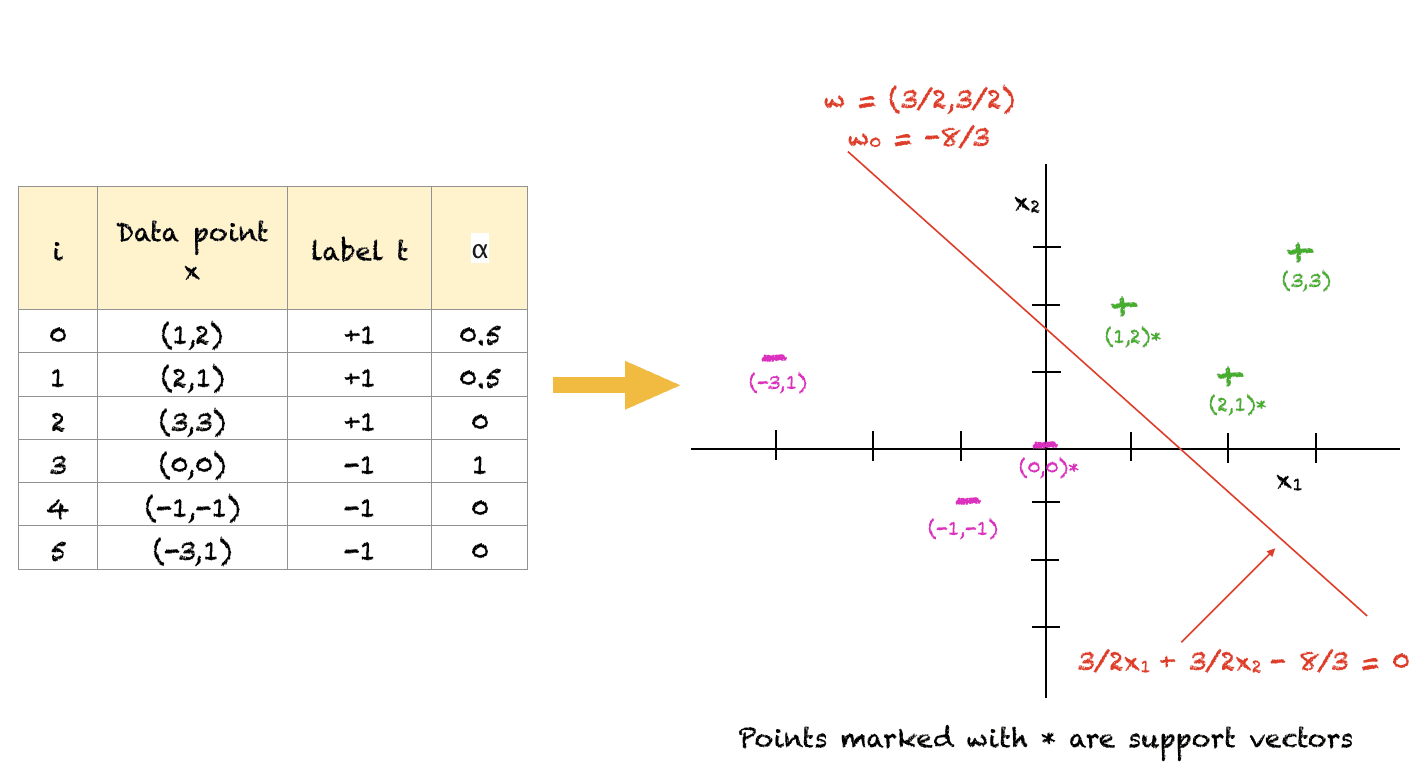

Pour l’ensemble de points ci-dessus, nous pouvons voir que (1,2), (2,1) et (0,0) sont les points les plus proches de l’hyperplan de séparation et agissent donc comme des vecteurs de support. Les points éloignés de la frontière (par exemple (-3,1)) ne jouent aucun rôle dans la détermination de la classification des points.

Lectures complémentaires

Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.

Livres

Des articles

Sommaire

Dans ce tutoriel, vous avez découvert comment utiliser la méthode des multiplicateurs de Lagrange pour résoudre le problème de maximisation de la marge via un problème de programmation quadratique avec contraintes d’inégalité.

Concrètement, vous avez appris :

• L’expression mathématique d’un hyperplan linéaire séparateur
• La marge maximale comme solution d’un problème de programmation quadratique avec contrainte d’inégalité
• Comment trouver un hyperplan linéaire entre des exemples positifs et négatifs en utilisant la méthode des multiplicateurs de Lagrange

Avez-vous des questions sur le SVM abordé dans cet article ? Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.