[ad_1]
Avant l’introduction du modèle Transformer, l’utilisation de l’attention pour la traduction automatique neuronale était mise en œuvre par des architectures encodeur-décodeur basées sur RNN. Le modèle Transformer a révolutionné la mise en œuvre de l’attention en dispensant la récurrence et les circonvolutions et, alternativement, en s’appuyant uniquement sur un mécanisme d’auto-attention.
Nous allons d’abord nous concentrer sur le mécanisme d’attention de Transformer dans ce didacticiel, puis examiner le modèle Transformer dans un autre.
Dans ce tutoriel, vous découvrirez le mécanisme d’attention de Transformer pour la traduction automatique neuronale.
Après avoir terminé ce tutoriel, vous saurez :
- Comment l’attention Transformer différait de ses prédécesseurs.
- Comment le Transformer calcule une attention de produit à l’échelle.
- Comment le Transformer calcule l’attention multi-têtes.
Commençons.

Le mécanisme d’attention du transformateur
Photo d’Andreas Gücklhorn, certains droits réservés.
Présentation du didacticiel
Ce tutoriel est divisé en deux parties ; elles sont:
- Introduction à l’attention du transformateur
- L’attention du transformateur
- Attention au produit à l’échelle
- Attention multi-têtes
Conditions préalables
Pour ce tutoriel, nous supposons que vous êtes déjà familiarisé avec :
Introduction à l’attention du transformateur
Nous nous sommes, jusqu’à présent, familiarisés avec l’utilisation d’un mécanisme d’attention en conjonction avec une architecture encodeur-décodeur basée sur RNN. Nous avons vu que deux des modèles les plus populaires qui mettent en œuvre l’attention de cette manière sont ceux proposés par Bahdanau et al. (2014) et Luong et al. (2015).
L’architecture Transformer a révolutionné l’utilisation de l’attention en dispensant la récurrence et les circonvolutions, sur lesquelles les premiers s’étaient largement appuyés.
… le Transformer est le premier modèle de transduction reposant entièrement sur l’auto-attention pour calculer les représentations de son entrée et de sa sortie sans utiliser de RNN alignés sur la séquence ou de convolution.
– L’attention est tout ce dont vous avez besoin, 2017.
Dans leur article, Attention Is All You Need, Vaswani et al. (2017) expliquent que le modèle Transformer, alternativement, repose uniquement sur l’utilisation de l’auto-attention, où la représentation d’une séquence (ou d’une phrase) est calculée en reliant différents mots dans la même séquence.
L’auto-attention, parfois appelée intra-attention, est un mécanisme d’attention reliant différentes positions d’une même séquence afin de calculer une représentation de la séquence.
– L’attention est tout ce dont vous avez besoin, 2017.
L’attention du transformateur
Les principaux composants utilisés par l’attention du transformateur sont les suivants :
- $mathbf{q}$ et $mathbf{k}$ désignant des vecteurs de dimension, $d_k$, contenant respectivement les requêtes et les clés.
- $mathbf{v}$ désignant un vecteur de dimension, $d_v$, contenant les valeurs.
- $mathbf{Q}$, $mathbf{K}$ et $mathbf{V}$ désignant des matrices regroupant des ensembles de requêtes, de clés et de valeurs, respectivement.
- $mathbf{W}^Q$, $mathbf{W}^K$ et $mathbf{W}^V$ désignant les matrices de projection qui sont utilisées pour générer différentes représentations de sous-espace des matrices de requête, de clé et de valeur.
- $mathbf{W}^O$ désignant une matrice de projection pour la sortie multi-têtes.
En substance, la fonction attention peut être considérée comme un mappage entre une requête et un ensemble de paires clé-valeur, vers une sortie.
La sortie est calculée comme une somme pondérée des valeurs, où le poids attribué à chaque valeur est calculé par une fonction de compatibilité de la requête avec la clé correspondante.
– L’attention est tout ce dont vous avez besoin, 2017.
Vaswani et al. proposer un attention sur les produits scalaires à l’échelle, puis s’en servir pour proposer attention à plusieurs têtes. Dans le contexte de la traduction automatique neuronale, la requête, les clés et les valeurs qui sont utilisées comme entrées pour ces mécanismes d’attention, sont des projections différentes de la même phrase d’entrée.
Intuitivement, donc, les mécanismes d’attention proposés mettent en œuvre l’auto-attention en capturant les relations entre les différents éléments (dans ce cas, les mots) d’une même phrase.
Attention au produit scalaire à l’échelle
Le Transformer implémente une attention de produit scalaire échelonnée, qui suit la procédure du mécanisme d’attention générale que nous avons vu précédemment.
Comme son nom l’indique, l’attention du produit scalaire à l’échelle calcule d’abord un produit scalaire pour chaque requête, $mathbf{q}$, avec toutes les clés, $mathbf{k}$. Il divise ensuite chaque résultat par $sqrt{d_k}$ et procède à l’application d’une fonction softmax. Ce faisant, il obtient les poids qui sont utilisés pour escalader les valeurs, $mathbf{v}$.
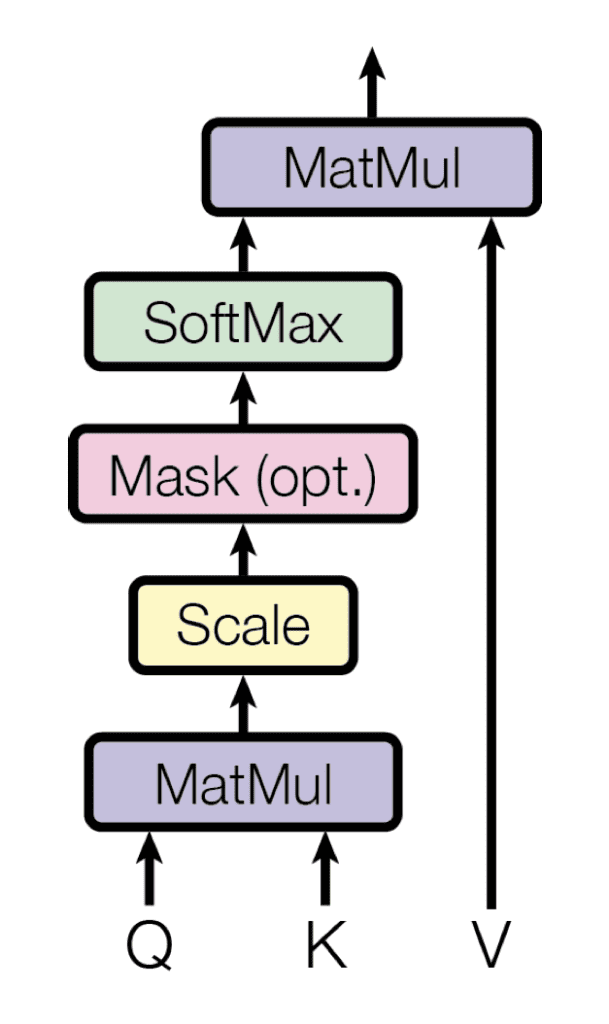
Attention au produit scalaire à l’échelle
Extrait de « L’attention est tout ce dont vous avez besoin »
En pratique, les calculs effectués par l’attention du produit scalaire à l’échelle peuvent être appliqués efficacement sur l’ensemble des requêtes simultanément. Pour ce faire, les matrices $mathbf{Q}$, $mathbf{K}$ et $mathbf{V}$, sont fournies en entrée de la fonction attention :
$$text{attention}(mathbf{Q}, mathbf{K}, mathbf{V}) = text{softmax} left( frac{QK^T}{sqrt{d_k}} à droite) V$$
Vaswani et al. expliquent que leur attention à l’échelle du produit scalaire est identique à l’attention multiplicative de Luong et al. (2015), à l’exception du facteur d’échelle ajouté de $tfrac{1}{sqrt{d_k}}$.
Ce facteur d’échelle a été introduit pour contrer l’effet de l’augmentation de l’amplitude des produits scalaires pour des valeurs élevées de $d_k$, où l’application de la fonction softmax renverrait alors des gradients extrêmement petits qui conduiraient au tristement célèbre problème des gradients de fuite. Le facteur d’échelle sert donc à tirer les résultats générés par la multiplication du produit scalaire vers le bas, évitant ainsi ce problème.
Vaswani et al. expliquent en outre que leur choix d’opter pour l’attention multiplicative au lieu de l’attention additive de Bahdanau et al. (2014), était basée sur l’efficacité de calcul associée au premier.
… l’attention aux produits scalaires est beaucoup plus rapide et plus efficace en termes d’espace dans la pratique, car elle peut être implémentée à l’aide d’un code de multiplication matriciel hautement optimisé.
– L’attention est tout ce dont vous avez besoin, 2017.
La procédure étape par étape pour calculer l’attention du produit à points échelonnés est donc la suivante :
- Calculez les scores d’alignement en multipliant l’ensemble des requêtes emballées dans la matrice, $mathbf{Q}$, avec les clés de la matrice, $mathbf{K}$. Si la matrice, $mathbf{Q}$, est de taille $m times d_k$ et la matrice, $mathbf{K}$, est de taille, $n times d_k$, alors la matrice résultante sera de taille $m fois n$ :
$$
mathbf{QK}^T =
begin{bmatrice}
e_{11} & e_{12} & dots & e_{1n} \
e_{21} & e_{22} & dots & e_{2n} \
vdots & vdots & ddots & vdots \
e_{m1} & e_{m2} & dots & e_{mn} \
end{bmatrice}
$$
- Mettez à l’échelle chacun des scores d’alignement de $tfrac{1}{sqrt{d_k}}$ :
$$
frac{mathbf{QK}^T}{sqrt{d_k}} =
begin{bmatrice}
tfrac{e_{11}}{sqrt{d_k}} & tfrac{e_{12}}{sqrt{d_k}} & dots & tfrac{e_{1n}}{sqrt{d_k}} \
tfrac{e_{21}}{sqrt{d_k}} & tfrac{e_{22}}{sqrt{d_k}} & dots & tfrac{e_{2n}}{sqrt{d_k}} \
vdots & vdots & ddots & vdots \
tfrac{e_{m1}}{sqrt{d_k}} & tfrac{e_{m2}}{sqrt{d_k}} & dots & tfrac{e_{mn}}{sqrt{d_k}} \
end{bmatrice}
$$
- Et suivez le processus de mise à l’échelle en appliquant une opération softmax afin d’obtenir un ensemble de poids :
$$
text{softmax} left( frac{mathbf{QK}^T}{sqrt{d_k}} right) =
begin{bmatrice}
text{softmax} left( tfrac{e_{11}}{sqrt{d_k}} right) & text{softmax} left( tfrac{e_{12}}{sqrt{d_k}} right) & dots & text{softmax} left( tfrac{e_{1n}}{sqrt{d_k}} right) \
text{softmax} left( tfrac{e_{21}}{sqrt{d_k}} right) & text{softmax} left( tfrac{e_{22}}{sqrt{d_k}} right) & dots & text{softmax} left( tfrac{e_{2n}}{sqrt{d_k}} right) \
vdots & vdots & ddots & vdots \
text{softmax} left( tfrac{e_{m1}}{sqrt{d_k}} right) & text{softmax} left( tfrac{e_{m2}}{sqrt{d_k}} right) & dots & text{softmax} left( tfrac{e_{mn}}{sqrt{d_k}} right) \
end{bmatrice}
$$
- Enfin, appliquez les poids résultants aux valeurs de la matrice, $mathbf{V}$, de taille, $n times d_v$ :
$$
begin{aligné}
& text{softmax} left( frac{mathbf{QK}^T}{sqrt{d_k}} right) cdot mathbf{V} \
=&
begin{bmatrice}
text{softmax} left( tfrac{e_{11}}{sqrt{d_k}} right) & text{softmax} left( tfrac{e_{12}}{sqrt{d_k}} right) & dots & text{softmax} left( tfrac{e_{1n}}{sqrt{d_k}} right) \
text{softmax} left( tfrac{e_{21}}{sqrt{d_k}} right) & text{softmax} left( tfrac{e_{22}}{sqrt{d_k}} right) & dots & text{softmax} left( tfrac{e_{2n}}{sqrt{d_k}} right) \
vdots & vdots & ddots & vdots \
text{softmax} left( tfrac{e_{m1}}{sqrt{d_k}} right) & text{softmax} left( tfrac{e_{m2}}{sqrt{d_k}} right) & dots & text{softmax} left( tfrac{e_{mn}}{sqrt{d_k}} right) \
end{bmatrice}
cdot
begin{bmatrice}
v_{11} & v_{12} & dots & v_{1d_v} \
v_{21} & v_{22} & dots & v_{2d_v} \
vdots & vdots & ddots & vdots \
v_{n1} & v_{n2} & dots & v_{nd_v} \
end{bmatrice}
end{aligné}
$$
Attention multi-têtes
S’appuyant sur leur fonction d’attention unique qui prend en entrée des matrices, $mathbf{Q}$, $mathbf{K}$ et $mathbf{V}$, comme nous venons de l’examiner, Vaswani et al. proposent également un mécanisme d’attention multi-têtes.
Leur mécanisme d’attention multi-têtes projette linéairement les requêtes, les clés et les valeurs $h$ fois, à chaque fois en utilisant une projection apprise différente. Le mécanisme d’attention unique est ensuite appliqué à chacune de ces projections $h$ en parallèle, pour produire des sorties $h$, qui à leur tour sont concaténées et projetées à nouveau pour produire un résultat final.
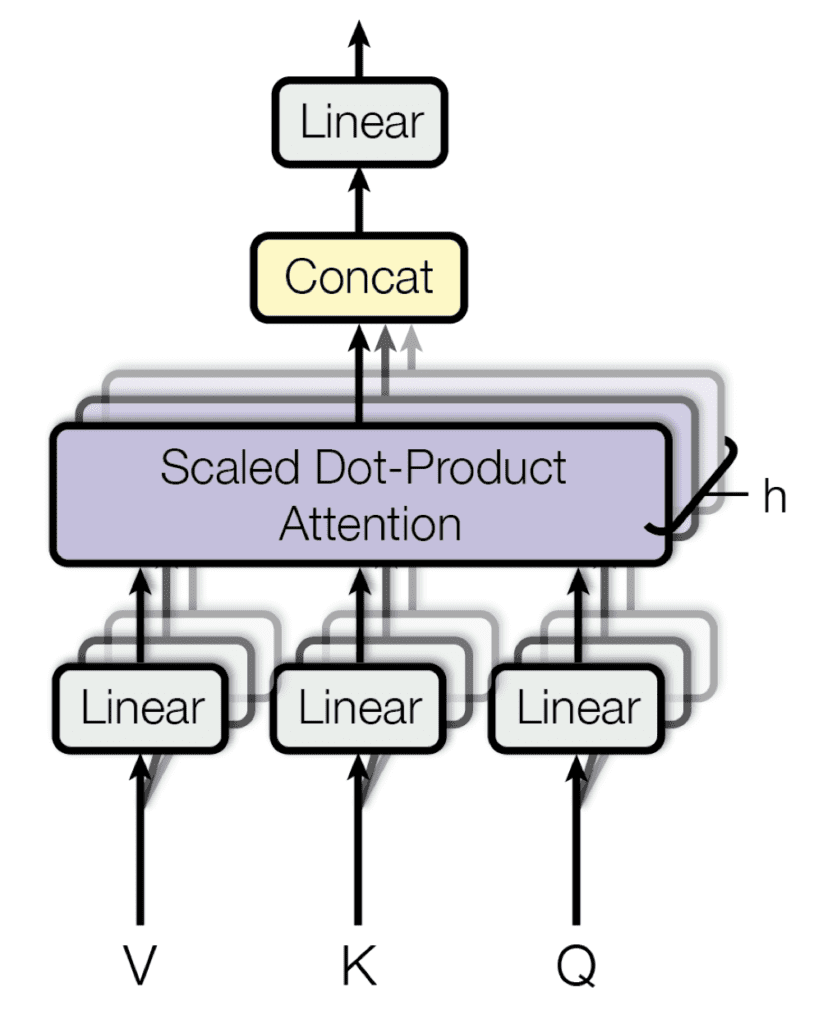
Attention multi-têtes
Extrait de « L’attention est tout ce dont vous avez besoin »
L’idée derrière l’attention multi-tête est de permettre à la fonction d’attention d’extraire des informations de différents sous-espaces de représentation, ce qui, autrement, ne serait pas possible avec une seule tête d’attention.
La fonction d’attention multi-têtes peut être représentée comme suit :
$$text{multihead}(mathbf{Q}, mathbf{K}, mathbf{V}) = text{concat}(text{head}_1, dots, text{head}_h) mathbf{W}^O$$
Ici, chaque $text{head}_i$, $i = 1, dots, h$, implémente une seule fonction d’attention caractérisée par ses propres matrices de projection apprises :
$$text{head}_i = text{attention}(mathbf{QW}^Q_i, mathbf{KW}^K_i, mathbf{VW}^V_i)$$
La procédure étape par étape pour calculer l’attention multi-tête est donc la suivante :
- Calculer les versions projetées linéairement des requêtes, des clés et des valeurs par une multiplication avec les matrices de poids respectives, $mathbf{W}^Q_i$, $mathbf{W}^K_i$ et $mathbf{W}^V_i$ , un pour chaque $text{head}_i$.
- Appliquez la fonction d’attention unique pour chaque tête en (1) multipliant les matrices de requêtes et de clés, (2) en appliquant les opérations de mise à l’échelle et de softmax, et (3) en pondérant la matrice de valeurs, pour générer une sortie pour chaque tête.
- Concaténer les sorties des têtes, $text{head}_i$, $i = 1, dots, h$.
- Appliquez une projection linéaire à la sortie concaténée via une multiplication avec la matrice de poids, $mathbf{W}^O$, pour générer le résultat final.
Lectures complémentaires
Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.
Livres
Papiers
Sommaire
Dans ce didacticiel, vous avez découvert le mécanisme d’attention de Transformer pour la traduction automatique neuronale.
Concrètement, vous avez appris :
- Comment l’attention Transformer différait de ses prédécesseurs.
- Comment le Transformer calcule une attention de produit à l’échelle.
- Comment le Transformer calcule l’attention multi-têtes.
Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.