Dernière mise à jour le 19 août 2021

La règle de la chaîne est une règle dérivée importante qui nous permet de travailler avec des fonctions composites. Il est essentiel pour comprendre le fonctionnement de l’algorithme de rétropropagation, qui applique largement la règle de la chaîne afin de calculer le gradient d’erreur de la fonction de perte par rapport à chaque poids d’un réseau de neurones. Nous nous appuierons sur notre introduction précédente à la règle de la chaîne, en nous attaquant à des fonctions plus difficiles.

Dans ce tutoriel, vous découvrirez comment appliquer la règle de calcul en chaîne à des fonctions difficiles.

Après avoir terminé ce tutoriel, vous saurez :

• Le processus d’application de la règle de la chaîne aux fonctions univariées peut être étendu aux fonctions multivariées.
• L’application de la règle de la chaîne suit un processus similaire, quelle que soit la complexité de la fonction : prenez d’abord la dérivée de la fonction externe, puis déplacez-vous vers l’intérieur. En cours de route, l’application d’autres règles dérivées pourrait être nécessaire.
• L’application de la règle de la chaîne aux fonctions multivariées nécessite l’utilisation de dérivées partielles.

Commençons.

Présentation du didacticiel

Ce tutoriel est divisé en deux parties ; ils sont:

• La règle de la chaîne sur les fonctions univariées
• La règle de la chaîne sur les fonctions multivariées

Conditions préalables

Pour ce tutoriel, nous supposons que vous savez déjà ce que sont :

Vous pouvez revoir ces concepts en cliquant sur les liens ci-dessus.

La règle de la chaîne sur les fonctions univariées

Nous avons déjà découvert la règle de la chaîne pour les fonctions univariées et multivariées, mais nous n’avons vu jusqu’à présent que quelques exemples simples. Voyons quelques plus difficiles ici. Nous commencerons d’abord par les fonctions univariées, puis appliquerons ce que nous apprenons aux fonctions multivariées.

EXEMPLE 1: Relevons un peu la barre en considérant la fonction composite suivante :

Nous pouvons séparer la fonction composite dans la fonction interne, F(X) = X² – 10, et la fonction extérieure, g(X) =X = (X)^1/2. La sortie de la fonction interne est désignée par la variable intermédiaire, vous, et sa valeur sera introduite dans l’entrée de la fonction externe.

La première étape consiste à trouver la dérivée de la partie externe de la fonction composite, tout en ignorant tout ce qui se trouve à l’intérieur. Pour cela, on peut appliquer la règle de puissance :

dh / du = (1/2) (X² – dix)^-1/2

L’étape suivante consiste à trouver la dérivée de la partie interne de la fonction composite, cette fois en ignorant tout ce qui se trouve à l’extérieur. Nous pouvons également appliquer la règle de puissance ici :

du / dx = 2X

En rassemblant les deux parties et en simplifiant, nous avons :

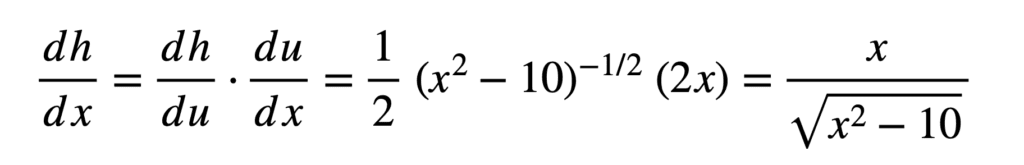
EXEMPLE 2: Répétons la procédure, cette fois avec une fonction composite différente :

Nous utiliserons à nouveau, vous, la sortie de la fonction interne, en tant que variable intermédiaire.

La fonction externe dans ce cas est, cos X. Trouver sa dérivée, encore une fois en ignorant l’intérieur, nous donne :

dh / du = (cos(X³ – 1))’ = -sin(X³ – 1)

La fonction interne est, X³ – 1. Ainsi, sa dérivée devient :

du / dx = (X³ – 1)’ = 3X²

En mettant les deux parties ensemble, on obtient la dérivée de la fonction composée :

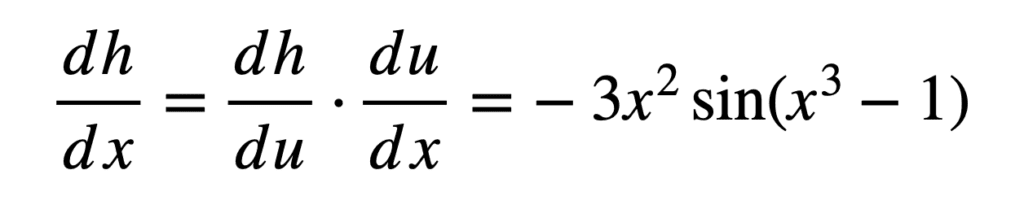
EXEMPLE 3: Relevons maintenant un peu plus la barre en considérant une fonction composite plus complexe :

Si nous observons cela de près, nous réalisons que non seulement nous avons des fonctions imbriquées pour lesquelles nous devrons appliquer la règle de chaîne plusieurs fois, mais nous avons également un produit auquel nous devrons appliquer la règle de produit.

Nous trouvons que la fonction la plus externe est un cosinus. Pour trouver sa dérivée par la règle de la chaîne, nous utiliserons la variable intermédiaire, vous:

dh / du = (cos(X (X² – 10) ))’ = -sin(X (X² – dix) )

A l’intérieur du cosinus, nous avons le produit, X (x² – 10), auquel nous appliquerons la règle du produit pour trouver sa dérivée (notez que nous nous déplaçons toujours de l’extérieur vers l’intérieur, afin de découvrir l’opération qui doit être abordée ensuite) :

du / dx = (X (x² – 10) )’ = (x² – 10) + X ( (x² – dix) )’

L’une des composantes du terme résultant est, ( √(x² – 10) )’, auquel nous appliquerons à nouveau la règle de la chaîne. En effet, nous l’avons déjà fait ci-dessus, et nous pouvons donc simplement réutiliser le résultat :

( (x² – 10) )’ = X (X² – dix)^-1/2

En mettant toutes les parties ensemble, on obtient la dérivée de la fonction composite :

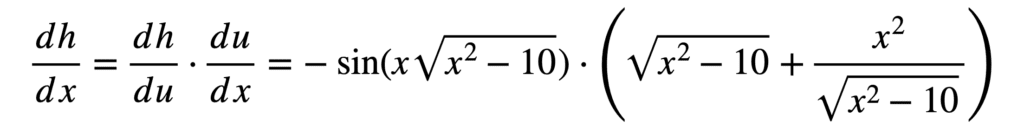
Cela peut être simplifié davantage en :

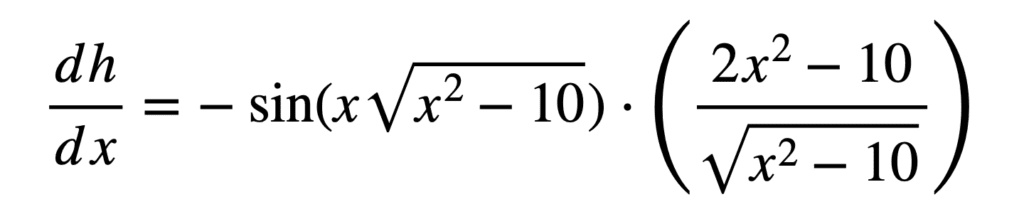
La règle de la chaîne sur les fonctions multivariées

EXEMPLE 4: Supposons que nous soyons maintenant présentés par une fonction multivariée de deux variables indépendantes, s et t, chacune de ces variables étant dépendante de deux autres variables indépendantes, X et oui:

h = g(s, t) = s² + t³

Où les fonctions, s = xy, et t = 2X – oui.

La mise en œuvre de la règle de la chaîne nécessite ici le calcul de dérivées partielles, car nous travaillons avec plusieurs variables indépendantes. Par ailleurs, s et t agira également comme nos variables intermédiaires. Les formules avec lesquelles nous allons travailler, définies par rapport à chaque entrée, sont les suivantes :

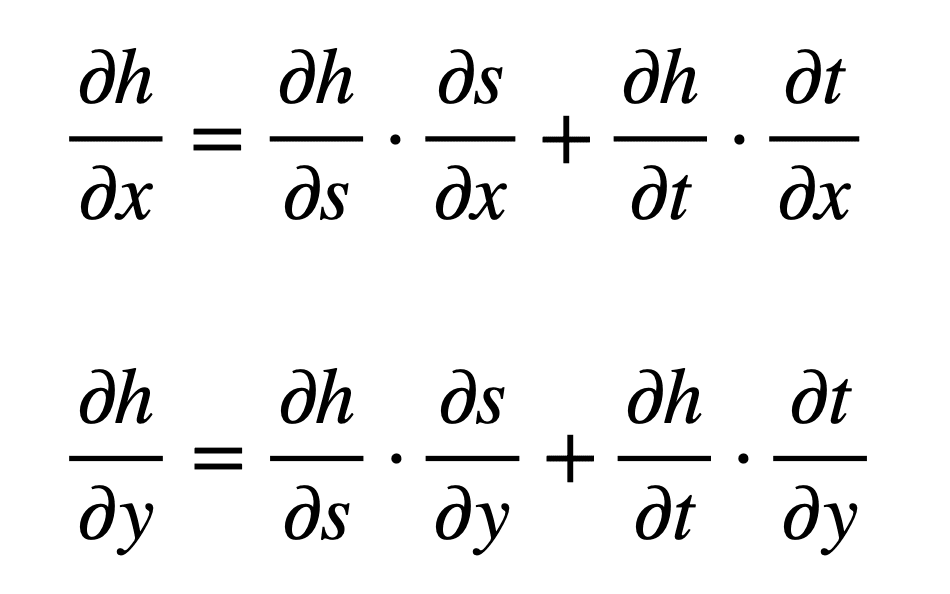
A partir de ces formules, nous pouvons voir que nous aurons besoin de trouver six dérivées partielles différentes :

Nous pouvons maintenant procéder à la substitution de ces termes dans les formules pour ∂h /X et ??h /oui:

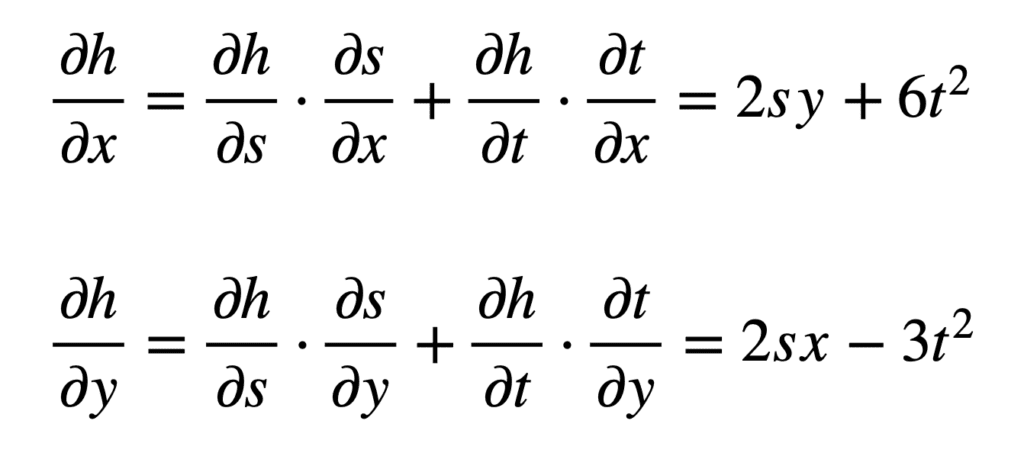
Et par la suite se substituer à s et t pour trouver les dérivées :

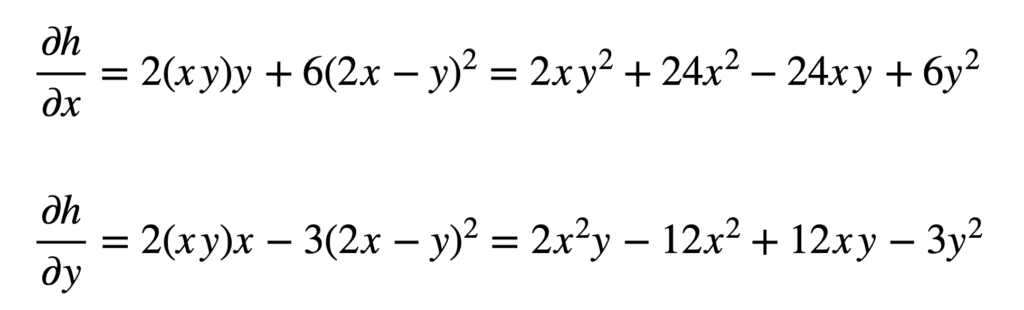
EXEMPLE 5: Répétons cela encore une fois, cette fois avec une fonction multivariée de trois variables indépendantes, $r$, $s$ et $t$, chacune de ces variables étant dépendante de deux autres variables indépendantes, $x$ et $y$ :
$$h=g(r,s,t)=r^2-rs+t^3$$
Où les fonctions $r = x cos y$, $s=xe^y$ et $t=x+y$.

Cette fois, $r$, $s$ et $t$ agiront comme nos variables intermédiaires. Les formules avec lesquelles nous allons travailler, définies par rapport à chaque entrée, sont les suivantes :

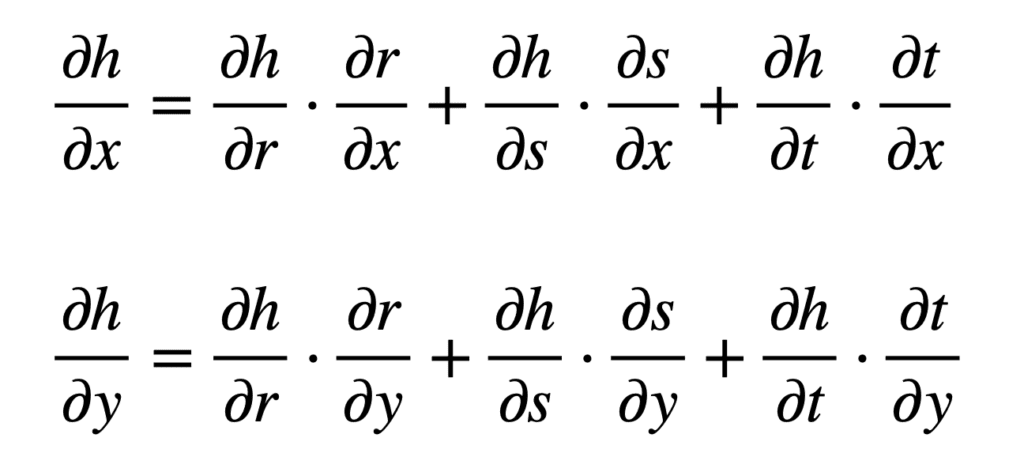
A partir de ces formules, nous pouvons voir qu’il va maintenant falloir trouver neuf dérivées partielles différentes :

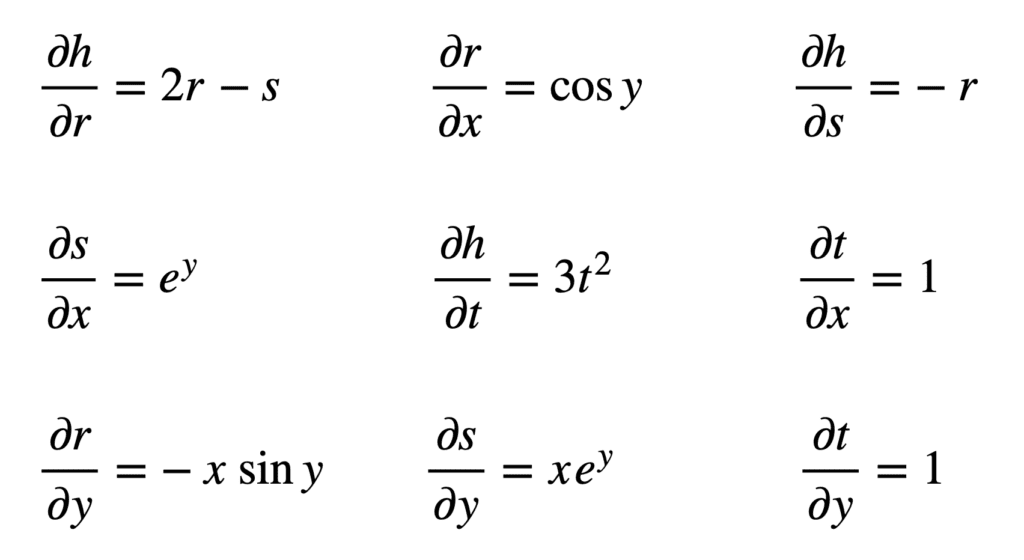
Encore une fois, nous procédons à la substitution de ces termes dans les formules pour ∂h /X et ??h /oui:

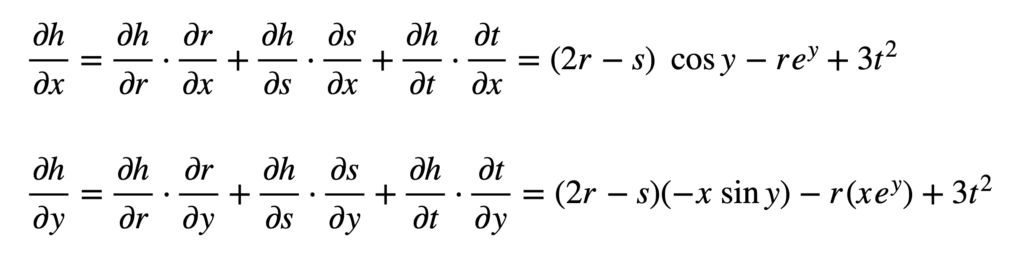
Et par la suite, remplacez $r$, $s$ et $t$ pour trouver les dérivées :

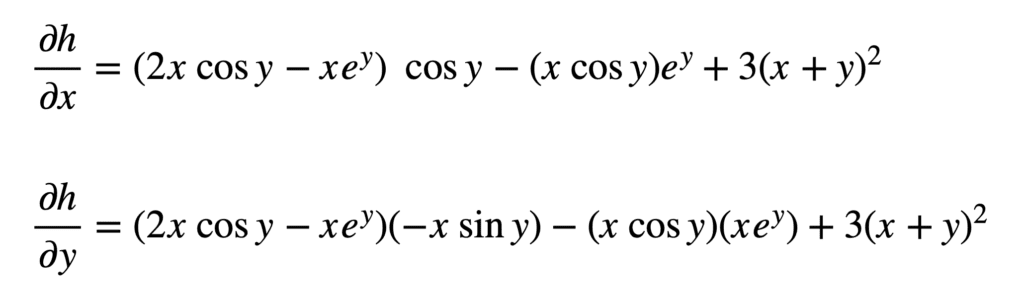
Ce qui peut être simplifié un peu plus (indice : appliquer l’identité trigonométrique $2sin ycos y=sin 2y$ à $partial h/partial y$) :

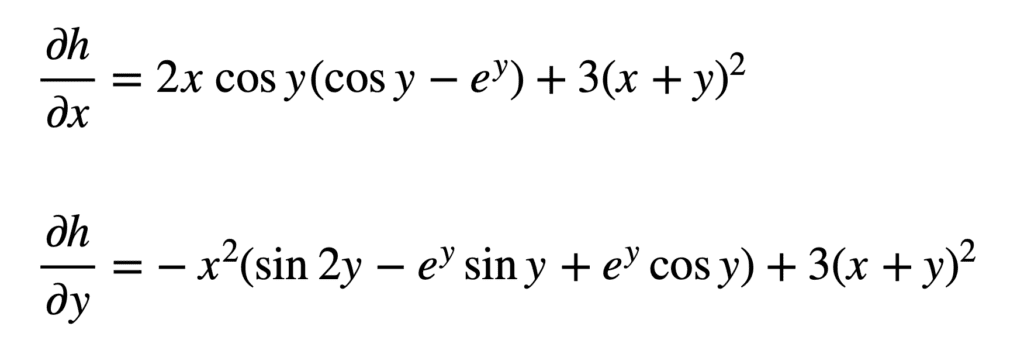
Quelle que soit la complexité de l’expression, la procédure à suivre reste similaire :

Votre dernier calcul vous indique la première chose à faire.

– Page 143, Calcul pour les nuls, 2016.

Par conséquent, commencez par vous attaquer d’abord à la fonction extérieure, puis passez à la suivante vers l’intérieur. Vous devrez peut-être appliquer d’autres règles en cours de route, comme nous l’avons vu pour l’exemple 3. N’oubliez pas de prendre les dérivées partielles si vous travaillez avec des fonctions multivariées.

Lectures complémentaires

Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.

Livres

Résumé

Dans ce didacticiel, vous avez découvert comment appliquer la règle de calcul en chaîne à des fonctions difficiles.

Concrètement, vous avez appris :

• Le processus d’application de la règle de la chaîne aux fonctions univariées peut être étendu aux fonctions multivariées.
• L’application de la règle de la chaîne suit un processus similaire, quelle que soit la complexité de la fonction : prenez d’abord la dérivée de la fonction externe, puis déplacez-vous vers l’intérieur. En cours de route, l’application d’autres règles dérivées pourrait être nécessaire.
• L’application de la règle de la chaîne aux fonctions multivariées nécessite l’utilisation de dérivées partielles.

Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.