Une telle fonction linéaire peut être représentée par l’équation d’une droite ayant une pente, m, et une ordonnée à l’origine, c:

oui = mx + c

Faire varier chacun des paramètres, m et c, produit différents modèles linéaires qui définissent différents mappages d’entrée-sortie.

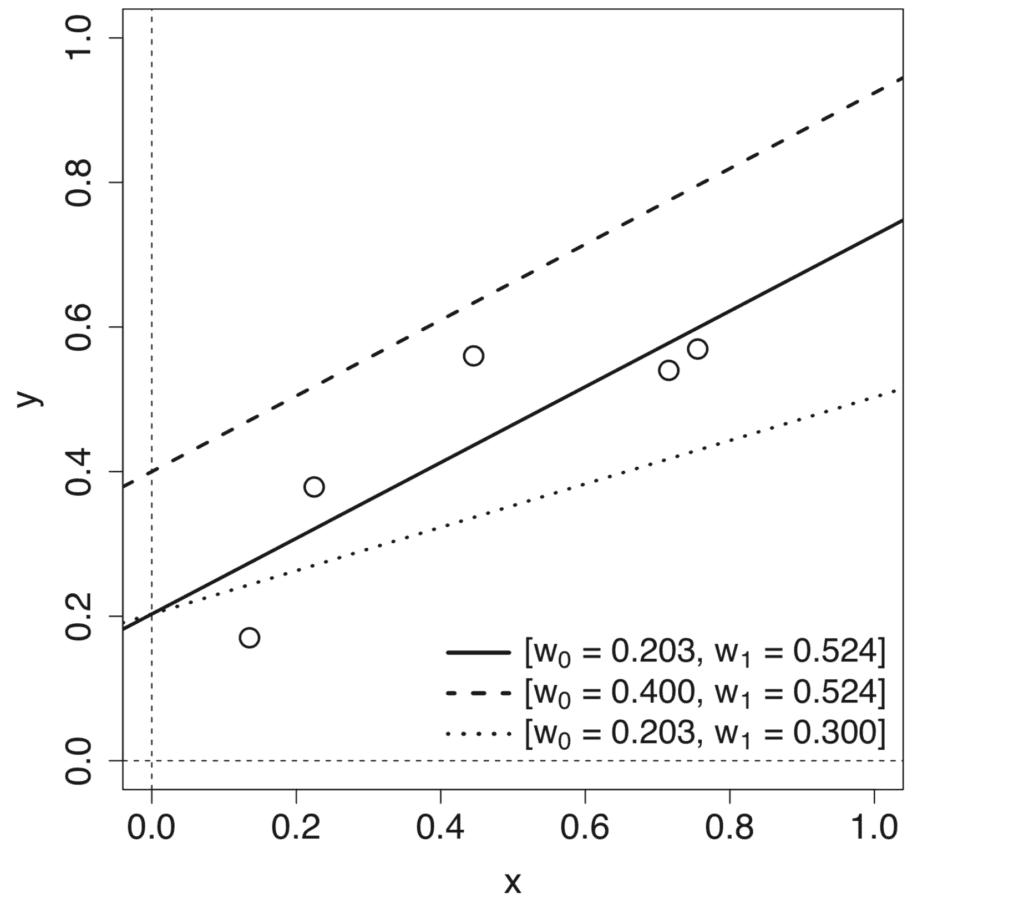
Tracé linéaire de différents modèles de ligne produit en faisant varier la pente et l’interception
Tiré de Deep Learning

Le processus d’apprentissage de la fonction de mappage implique donc l’approximation de ces paramètres de modèle, ou poids, qui se traduisent par l’erreur minimale entre les sorties prédites et cibles. Cette erreur est calculée au moyen d’une fonction de perte, d’une fonction de coût ou d’une fonction d’erreur, souvent utilisées de manière interchangeable, et le processus de minimisation de la perte est appelé optimisation des fonctions.

Nous pouvons appliquer le calcul différentiel au processus d’optimisation des fonctions.

Afin de mieux comprendre comment le calcul différentiel peut être appliqué à l’optimisation des fonctions, revenons à notre exemple spécifique d’avoir une fonction de mappage linéaire.

Disons que nous avons un ensemble de données d’entités à entrée unique, X, et leurs résultats cibles correspondants, oui. Afin de mesurer l’erreur sur l’ensemble de données, nous prendrons la somme des erreurs au carré (SSE), calculée entre les sorties prédites et cibles, comme fonction de perte.

Effectuer un balayage des paramètres sur différentes valeurs pour les poids du modèle, w₀ = m et w₁ = c, génère des profils d’erreur individuels de forme convexe.

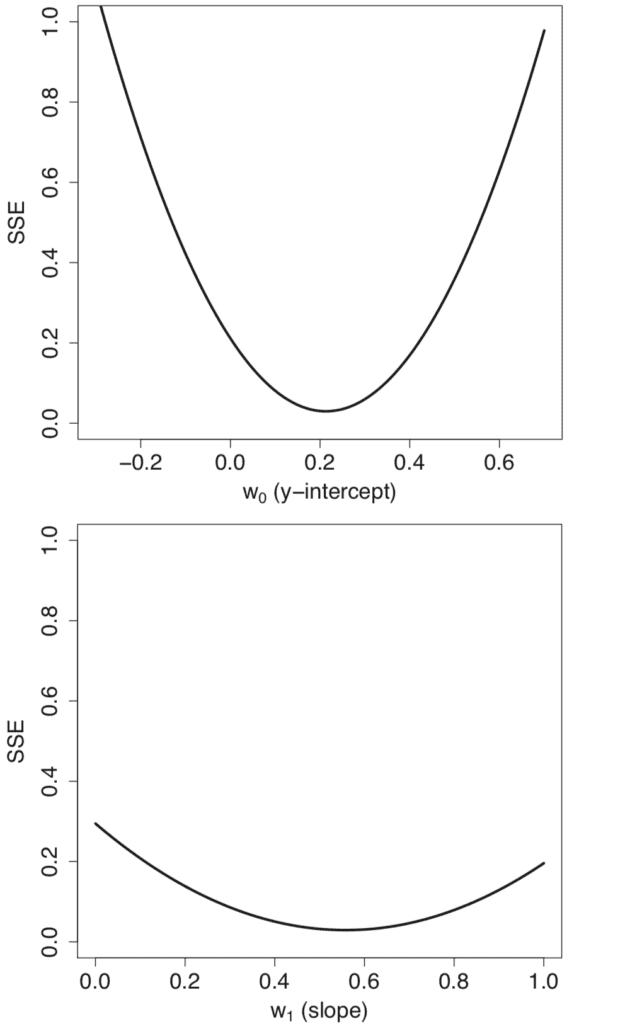
Profils linéaires d’erreur (SSE) générés lors du balayage sur une plage de valeurs pour la pente et l’interception
Tiré de Deep Learning

La combinaison des profils d’erreur individuels génère une surface d’erreur tridimensionnelle qui est également de forme convexe. Cette surface d’erreur est contenue dans un espace de poids, qui est défini par les plages de valeurs balayées pour les poids du modèle, w₀ et w₁.

Tracé tridimensionnel de la surface d’erreur (SSE) générée lorsque la pente et l’interception varient à la fois
Tiré de Deep Learning

Se déplacer dans cet espace de poids équivaut à se déplacer entre différents modèles linéaires. Notre objectif est d’identifier le modèle qui correspond le mieux aux données parmi toutes les alternatives possibles. Le meilleur modèle est caractérisé par l’erreur la plus faible sur l’ensemble de données, qui correspond au point le plus bas sur la surface d’erreur.

Une surface d’erreur convexe ou en forme de bol est incroyablement utile pour apprendre une fonction linéaire pour modéliser un ensemble de données, car cela signifie que le processus d’apprentissage peut être défini comme une recherche du point le plus bas sur la surface d’erreur. L’algorithme standard utilisé pour trouver ce point le plus bas est connu sous le nom de descente de gradient.

Page 194, Apprentissage en profondeur, 2019.

L’algorithme de descente de gradient, comme l’algorithme d’optimisation, cherchera à atteindre le point le plus bas sur la surface d’erreur en suivant son gradient en descente. Cette descente est basée sur le calcul du gradient, ou pente, de la surface d’erreur.

C’est là qu’intervient le calcul différentiel.

Le calcul, et en particulier la différenciation, est le domaine des mathématiques qui traite des taux de changement.

Page 198, Apprentissage en profondeur, 2019.

Plus formellement, désignons la fonction que l’on souhaite optimiser par :

erreur = F(poids)

En calculant le taux de variation, ou la pente, de l’erreur par rapport aux poids, l’algorithme de descente de gradient peut décider de la manière de modifier les poids afin de continuer à réduire l’erreur.

Pourquoi le calcul dans l’apprentissage automatique fonctionne

La fonction d’erreur que nous avons envisagé d’optimiser est relativement simple, car convexe et caractérisée par un seul minimum global.

Néanmoins, dans le contexte de l’apprentissage automatique, nous devons souvent optimiser des fonctions plus complexes qui peuvent rendre la tâche d’optimisation très difficile. L’optimisation peut devenir encore plus difficile si l’entrée de la fonction est également multidimensionnelle.

Calculus nous fournit les outils nécessaires pour relever ces deux défis.

Supposons que nous ayons une fonction plus générique que nous souhaitons minimiser, et qui prend une entrée réelle, X, pour produire une sortie réelle, oui:

oui = f(X)

Calculer le taux de variation à différentes valeurs de X est utile car il nous donne une indication des changements que nous devons appliquer à X, afin d’obtenir les changements correspondants de oui.

Puisque nous minimisons la fonction, notre objectif est d’atteindre un point qui obtient une valeur aussi faible de f(X) dans la mesure du possible qui se caractérise également par un taux de variation nul ; par conséquent, un minimum global. Selon la complexité de la fonction, cela peut ne pas être nécessairement possible car il peut y avoir de nombreux minima locaux ou points de selle dans lesquels l’algorithme d’optimisation peut rester coincé.

Dans le contexte de l’apprentissage en profondeur, nous optimisons des fonctions qui peuvent avoir de nombreux minima locaux qui ne sont pas optimaux, et de nombreux points de selle entourés de régions très plates.

Page 84, Apprentissage en profondeur, 2017.

Ainsi, dans le cadre du deep learning, nous acceptons souvent une solution sous-optimale qui ne correspond pas nécessairement à un minimum global, tant qu’elle correspond à une valeur très faible de f(X).

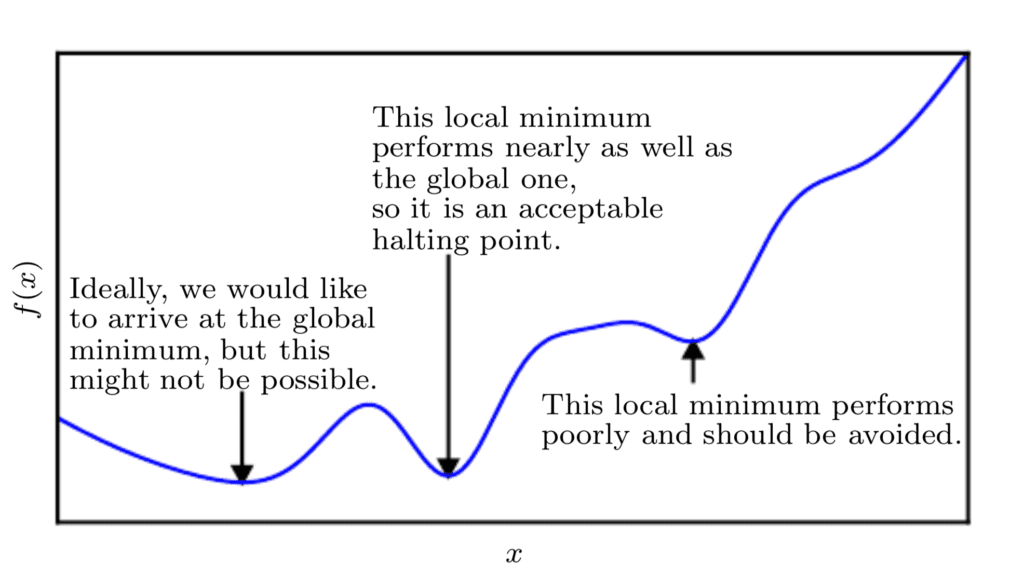
Fonction de tracé linéaire de la fonction de coût pour minimiser l’affichage des minima locaux et globaux
Tiré de Deep Learning

Si la fonction avec laquelle nous travaillons prend plusieurs entrées, le calcul nous fournit également le concept de dérivées partielles; ou en termes plus simples, une méthode pour calculer le taux de variation de oui en ce qui concerne les changements dans chacune des entrées, X_je, tout en maintenant les entrées restantes constantes.

C’est pourquoi chacun des poids est mis à jour indépendamment dans l’algorithme de descente de gradient : la règle de mise à jour des poids dépend de la dérivée partielle du SSE pour chaque poids, et comme il existe une dérivée partielle différente pour chaque poids, il existe un poids distinct règle de mise à jour pour chaque poids.

Page 200, Apprentissage en profondeur, 2019.

Ainsi, si l’on considère à nouveau la minimisation d’une fonction d’erreur, le calcul de la dérivée partielle de l’erreur par rapport à chaque poids spécifique permet que chaque poids soit mis à jour indépendamment des autres.

Cela signifie également que l’algorithme de descente de gradient peut ne pas suivre une trajectoire rectiligne sur la surface d’erreur. Au contraire, chaque poids sera mis à jour proportionnellement au gradient local de la courbe d’erreur. Par conséquent, un poids peut être mis à jour d’une plus grande quantité qu’un autre, autant que nécessaire pour que l’algorithme de descente de gradient atteigne le minimum de la fonction.

Lectures complémentaires

Cette section fournit plus de ressources sur le sujet si vous cherchez à approfondir.

Livres

Résumé

Dans ce didacticiel, vous avez découvert le rôle essentiel du calcul dans l’apprentissage automatique.

Concrètement, vous avez appris :

• Le calcul joue un rôle essentiel dans la compréhension du fonctionnement interne des algorithmes d’apprentissage automatique, tels que l’algorithme de descente de gradient qui minimise une fonction d’erreur basée sur le calcul du taux de changement.
• Le concept du taux de changement dans le calcul peut également être exploité pour minimiser des fonctions objectifs plus complexes qui ne sont pas nécessairement de forme convexe.
• Le calcul de la dérivée partielle, un autre concept important en calcul, nous permet de travailler avec des fonctions qui prennent plusieurs entrées.

Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.